Classificazione

Un ruolo predominante nella Visione Artificiale rivestono le tecniche di Classificazione e di machine learning. La grande quantità di informazione che si può estrarre da un sensore video supera di gran lunga in quantità quella che si può ottenere da altri sensori ma richiedono tecniche complesse che permettano di sfruttare questa ricchezza di informazione.

Come già detto in precedenza, statistica, classificazione e fitting di modelli si possono vedere di fatto come diverse facce di un unico argomento. La statistica ricerca il modo più corretto dal punto di vista bayesiano per estrarre i parametri (dello stato o modello) nascosti di un sistema, affetto eventualmente da rumore, cercando, dati gli ingressi, di restituire l'uscita più probabile mentre la classificazione propone tecniche e modi su come modellare il sistema in maniera efficiente. Infine se si conoscesse il modello esatto che sottostà a un sistema fisico, qualunque problema di classificazione si ricondurrebbe a un problema di ottimizzazione. Per queste ragioni non è pertanto facile ne netto capire dove finisca un argomento e inizi l'altro.

Il problema della classificazione si riconduce a quello di ricavare i parametri di un modello generico che permetta di generalizzare il problema avendo a disposizione un numero limitato di esempi.

Un classificatore può essere visto in due modi, a seconda di che tipo di informazione tale sistema voglia fornire:

1. come funzione di “verosomiglianza” verso un modello, come in equazione (4.1);
2. come partizionamento dello spazio degli ingressi, come in equazione (4.2).

Nel primo caso un classificatore viene rappresentato da una generica funzione

$$f: \mathbb{R}^{n} \to \mathbb{R}^{m}$$ (4.1)

che permette di associare all'elemento $\mathbf {x}$ in ingresso, formato dalle $n$ caratteristiche rappresentanti l'esempio da classificare, dei valore di confidenza rispetto alle possibili $\{y_1,\ldots,y_m\}$ classi di uscita (categorie):

$$f(\mathbf{x}) = \left( p(y_1\vert\mathbf{x}), \ldots, p(y_m\vert\mathbf{x}) \right)$$

ovvero la probabilità che l'oggetto osservato sia proprio $y_i$ data la quantità osservata $\mathbf {x}$.

A causa sia dell'infinità delle possibili funzioni sia della mancanza di ulteriori informazioni specifiche sulla forma del problema, la funzione $f$ non potrà essere un funzione ben specifica ma verrà rappresentata da un modello a parametri nella forma

$$\mathbf{y} = f(\mathbf{x}, \boldsymbol\beta)$$

dove $\mathbf{y} \in \mathbb{R}^{m}$ è lo spazio degli output, $\mathbf{x} \in \mathbb{R}^{n}$ spazio degli input mentre $\boldsymbol\beta$ sono i parametri del modello $f$ da determinare nella fase di addestramento.

La fase di addestramento si basa su un insieme di esempi (training set) formato da coppie $(\mathbf{x}_i, \mathbf{y}_i)$ e attraverso questi esempi la fase di addestramento deve determinare i parametri $\boldsymbol\beta$ della funzione $f(\mathbf{x},\boldsymbol\beta)$ che minimizzino, sotto una determinata metrica (funzione di costo), l'errore sul training set stesso.

Per addestrare il classificatore bisogna pertanto individuare i parametri ottimi $\boldsymbol\beta$ che minimizzano l'errore nello spazio delle uscite: la classificazione è anche un problema di ottimizzazione. Per questa ragione machine learning, fitting di modelli e statistica risultano ambiti di ricerca strettamente legati. Le medesime considerazioni usate in Kalman o per Hough e tutto ciò detto nel capitolo di fitting di modelli ai minimi quadrati si possono usare per classificare e gli algoritmi specifici di classificazione possono essere usati ad esempio per adattare una serie di osservazioni affette da rumore a una curva.

Normalmente non è possibile produrre un insieme di addestramento completo: non è infatti sempre possibile ottenere qualsiasi tipo di associazione ingresso-uscita in modo da mappare in maniera sistematica tutto lo spazio degli input nello spazio degli output e, se ciò fosse anche possibile, risulterebbe comunque dispendioso disporre della memoria necessaria per rappresentare tali associazioni sotto forma di Look Up Table. Queste solo le principali ragioni dell'utilizzo di modelli nella classificazione.

Il fatto che il training set non possa coprire tutte le possibili combinazioni ingresso-uscita, combinato alla generazione di un modello ottimizzato verso tali dati incompleti, può provocare una non-generalizzazione dell'addestramento: elementi non presenti nell'insieme di addestramento potrebbero essere classificati in maniera errata a causa dell'eccessivo adattamento al training set (problema dell'overfitting). Questo fenomeno è causato normalmente da una fase di ottimizzazione che si preoccupa più di ridurre l'errore sulle uscite piuttosto che di generalizzare il problema.

Tornando ai modi per vedere un classificatore, risulta spesso più semplice e più generalizzante ricavare direttamente dai dati in ingresso una superficie in $\mathbb{R}^n$ che separi le categorie nello spazio n-dimensionale degli ingressi. Si può definire una nuova funzione $g$ che ad ogni gruppo di ingressi associ una ed una sola etichetta in uscita, nella forma

$$g: \mathbb{R}^{n} \to \mathbb{Y}=\{y_1, \ldots, y_m \}$$ (4.2)

Questo è il secondo modo di vedere un classificatore.

L'espressione (4.1) può essere sempre convertita nella forma (4.2) attraverso una votazione per maggioranza:

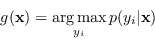$$g(\mathbf{x}) = \argmax_{y_i} p(y_i\vert\mathbf{x})$$ (4.3)

Il classificatore, sotto questo punto di vista, è una funzione che restituisce direttamente il simbolo più somigliante all'ingresso fornito. Il training set ora deve associare a ogni ingresso (ogni elemento dello spazio) una ed una sola classe $y \in \mathbb{Y}$ in uscita. Solitamente questo modo di vedere un classificatore permette di ridurre la complessità computazionale e l'utilizzo di risorse.

Se la funzione (4.1) rappresenta effettivamente una funzione di trasferimento, una risposta, la funzione (4.2) può essere vista come un partizionamento dello spazio $\mathbb{R}^{n}$ dove a regioni, generalmente molto complesse e non contigue dello spazio degli ingressi, è associata un'unica classe.

Per le motivazioni addotte in precedenza non è fisicamente possibile realizzare un classificatore ottimo (se non per problemi di dimensioni molto contenute o per modelli semplici e conosciuti perfettamente) ma esistono diversi classificatori general purpose che a seconda del problema e delle performance richieste possono considerarsi sub-ottimi. Nel caso dei classificatori (4.2) il problema è quello di ottenere un partizionamento ottimo dello spazio e pertanto è richiesto un set di primitive veloci e tali da non usare troppa memoria nel caso di alti valori di $n$, mentre nel caso (4.1) è richiesta espressamente una funzione che modelli molto bene il problema evitando però specializzazioni.

Le informazioni (features) che si possono estrarre da una immagine per permetterne la classificazione sono molteplici. In genere usare direttamente i toni di grigio/colore dell'immagine è raramente usato in applicazioni pratiche perché tali valori sono normalmente influenzati dalla luminosità della scena e sopratutto perché rappresenterebbero uno spazio di ingresso molto vasto, difficilmente gestibile. È necessario pertanto estrarre dalla parte di immagine da classificare delle informazioni essenziali (features) che ne descrivano l'aspetto al meglio. Per questa ragione, tutta la teoria mostrata in sezione 6 è ampiamente usata in machine learning. Sono ampiamente usati infatti, sia le feature di Haar grazie alla loro velocità di estrazione o gli Istogrammi dell'Orientazione del Gradiente (HOG, sez. 6.2) per la loro accuratezza. Come compromesso, e loro generalizzazione, tra le due classi di feature di recente sono state proposte le Feature su Canali Integrali (ICF, sez. 6.3).

Per ridurre la complessità del problema di classificazione questo può essere diviso in più strati da affrontare in maniera indipendente: un primo strato trasforma lo spazio degli ingressi nello spazio delle caratteristiche, mentre un secondo livello esegue la classificazione vera e propria partendo dallo spazio delle caratteristiche.

Sotto questa considerazione le tecniche di classificazione si possono dividere in 3 categorie principali:

Rule-based learning

In questo caso sia lo spazio delle caratteristiche che i parametri della funzione di classificazione sono decisi da un utente umano, senza sfruttare alcun insieme di dati o esempi di addestramento;

Machine Learning

La trasformazione tra spazio di ingressi a spazio delle caratteristiche è scelta dall'utente tra un insieme finito di funzioni, mentre l'estrazione dei parametri del modello è lasciata all'elaboratore analizzando gli esempi forniti;

Representation learning

Sia la trasformazione in spazio delle caratteristiche che l'estrazione dei parametri del modello sono attuati dal calcolatore.

Recentemente tecniche di Representation learning costruite con più strati in cascata tra loro (Deep Learning) hanno avuto molto successo a risolvere problemi di classificazione complesse.

Tra le tecniche per trasformare lo spazio di ingressi nello spazio delle caratteristiche è importante citare la PCA, tecnica lineare non supervisionata. La Principal Component Analysis (sezione 2.10.1) è una tecnica che permette di ridurre il numero di ingressi al classificatore, rimuovendo le componenti linearmente dipendenti o ininfluenti, riducendo pertanto la dimensione del problema cercando comunque di preservare al massimo l'informazione.

Per quanto riguarda i modelli e le tecniche di modellazione general purpose molto utilizzate sono

Regressione

una regressione di dati ad un modello è di fatto un classificatore. Di conseguenza, tutta la teoria del capitolo 3 può e deve essere usata per classificare dati;Tra

Neural Network

Le reti neurali permettono di generare funzioni di tipo (4.1) concatenando tra loro somme, moltiplicazioni e funzioni fortemente non lineari come le sigmoidi. Tecniche di regressione permettono di stimare i parametri di questo modello generico;

Classificatori Bayesiani

è possibile usare il teorema di Bayes direttamente come classificatore o per unire insieme più classificatori in modo da massimizzare la probabilità a posteriori di individuare la classe corretta (sezione 4.2);

Albero di decisione

dove i classificatori sono messi in cascata con altri classificatori (ed ogni nodo rappresenta un qualche attributo estratto dai dati in ingresso);

Decision Stump

albero di decisione degenere (1 nodo), permette di partizionare lo spazio delle features usando una semplice soglia, diventando cosı il più semplice classificatore di tipo (4.2) ed esempio di classificatore debole;

Ensemble Learning

Più classificatori deboli (weak) possono essere messi in relazione tra loro (Ensemble Learning, sezione 4.6) in modo da massimizzare qualche metrica globale (ad esempio il margine di separazione tra le classi). Di fatto non sono veri e propri classificatori ma sono tecniche per unire più classificatori semplici e generare un classificatore complesso (ensemble).

Figura: Esempio di Template Matching. L'approccio funziona bene sull'immagine di origine, ma non è possibile estenderlo ad altre immagini, soprattutto con variazioni di luminosità e scala sensibili.