Regolarizzazione L1 ed L2

La regolarizzazione L1 ed L2 consiste nell'inserire un termine aggiuntivo alla funzione costo, penalizzante per alcune configurazioni. Regolarizzare, per esempio, la funzione costo

$$S(\boldsymbol\beta, \mathbf{X}) = - \sum_i \log P (Y = y_i \vert \mathbf{x}_i ; \boldsymbol\beta)$$ (4.90)

significa aggiungere un termine, funzione solo di $\boldsymbol\beta$, in maniera da ottenere la nuova funzione costo del tipo

$$E(\boldsymbol\beta, \mathbf{X}) = S(\boldsymbol\beta, \mathbf{X}) + \lambda R(\boldsymbol\beta)$$ (4.91)

con $R(\boldsymbol\beta)$ una funzione regolarizzante.

Una funzione regolarizzante molto diffusa è

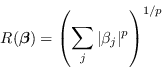$$R(\boldsymbol\beta) = \left( \sum_j \vert \beta_j \vert ^ p \right)^{1/p}$$ (4.92)

Valori comuni per $p$ sono $1$ o $2$ (per questo viene chiamata regolarizzazione L1 o L2). Quando $p=2$ può essere definita in letteratura anche come weight decay. Questo genere di funzioni di regolarizzazione penalizzano pertanto i parametri con valori troppi elevati.