Next: Le funzioni di attivazione Up: Classificazione Previous: AdaBoost e le sue
La ricerca sul Machine Learning (e in generale la Visione Artificiale) ha sempre cercato di trarre spunto per lo sviluppo degli algoritmi dal cervello umano.
Le reti neurali artificiali (artificial neural networks ANN) si basano sul concetto di “neurone artificiale” ovvero una struttura che, similarmente ai neuroni degli esseri viventi, applicano una trasformazione non lineare (detta funzione di attivazione) ai contributi pesati dei diversi ingressi del neurone:
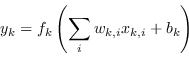 |
(4.80) |
La rete neurale più semplice, composta da uno stadio di ingresso e uno stadio di uscita, è assimilabile al modello di perceptrone (perceptron) introdotto da Rosenblatt nel 1957. Similarmente al cervello degli esseri viventi, una rete neurale artificiale consiste nella connessione di diversi neuroni artificiali.
La geometria di una rete neurale feedforward, la topologia normalmente utilizzata in applicazioni pratiche, è quella del MultiLayer Perceptron MLP e consiste nella combinazione di molteplici strati nascosti di neuroni che collegano lo stadio degli ingressi con lo stadio delle uscite, stadio che sarà l'ingresso dello strato successivo. Un perceptrone multistrato è assimilabile a una funzione
La fase di addestramento consiste nello stimare i pesi ![]() che minimizzano l'errore tra le etichette di addestramento e i valori predetti dalla rete
che minimizzano l'errore tra le etichette di addestramento e i valori predetti dalla rete
![]() :
:
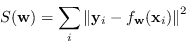 |
(4.81) |