Next: Reti Neurali Up: Ensemble Learning Previous: ADAptive BOOSTing
Il problema di Boosting si può generalizzare e può essere visto come un problema dove è necessario cercare dei predittori
![]() che minimizzino la funzione costo globale:
che minimizzino la funzione costo globale:
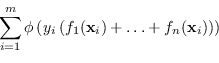 |
(4.65) |
Dal punto di vista analitico, AdaBoost è un esempio di ottimizzatore a discesa del gradiente (coordinate-wise gradient descent) che minimizza la potential function
![]() , ottimizzando un coefficiente
, ottimizzando un coefficiente ![]() per volta (LS10), come si vede dall'equazione (4.54).
per volta (LS10), come si vede dall'equazione (4.54).
Un elenco, non esaustivo ma che permette di fare luce su alcune peculiarità di questa tecnica, delle varianti di AdaBoost è:
AdaBoost può essere esteso anche a casi di classificatori con astensione, dove le uscite possibili sono
![]() .
Ampliando la definizione (4.57), per semplicità si indichino con
.
Ampliando la definizione (4.57), per semplicità si indichino con ![]() gli insuccessi,
gli insuccessi, ![]() le astensioni e
le astensioni e ![]() i successi del classificatore
i successi del classificatore ![]() .
.
Anche in questo caso ![]() assume il minimo con lo stesso valore di
assume il minimo con lo stesso valore di ![]() del caso senza astensione, cfr. (4.63),
e con tale scelta
del caso senza astensione, cfr. (4.63),
e con tale scelta ![]() varrebbe
varrebbe
| (4.66) |
Tuttavia esiste una scelta più conservativa di ![]() proposta da Freund e Shapire
proposta da Freund e Shapire
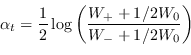 |
(4.67) |
Real AdaBoost generalizza il caso precedente ma soprattutto generalizza lo stesso modello additivo esteso (FHT00).
Invece che usare ipotesi dicotomiche ![]() e associare ad esse un peso
e associare ad esse un peso ![]() si cerca direttamente la feature
si cerca direttamente la feature ![]() che minimizza l'equazione (4.54).
che minimizza l'equazione (4.54).
Real AdaBoost permette di usare classificatori deboli che forniscono la distribuzione di probabilità
![]() , probabilità che la classe
, probabilità che la classe ![]() sia effettivamente
sia effettivamente ![]() data l'osservazione della caratteristica
data l'osservazione della caratteristica ![]() .
.
Data una distribuzione di probabilità ![]() , la feature
, la feature ![]() , che minimizza l'equazione (4.54), è
, che minimizza l'equazione (4.54), è
Sia Discrete che Real AdaBoost, scegliendo un classificatore debole che rispetti l'equazione 4.68, fanno in modo che AdaBoost converga asintoticamente a
Real AdaBoost può essere usato anche con un classificatore discreto come il Decision Stump.
Applicando direttamente l'equazione (4.68) ai due possibili stati di uscita del Decision Stump (risulta comunque facile ottenere il minimo di ![]() per via algebrica) le risposte del classificatore devono assumere i valori
per via algebrica) le risposte del classificatore devono assumere i valori
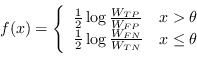 |
(4.70) |
| (4.71) |
Gentle AdaBoost generalizza ulteriormente il concetto di Ensemble Learning a modello additivo (FHT00) usando una regressione con passi tipici dei metodi di Newton:
| (4.72) |
L'ipotesi ![]() , da aggiungere al modello additivo all'iterazione
, da aggiungere al modello additivo all'iterazione ![]() , viene scelta fra tutte le possibili ipotesi
, viene scelta fra tutte le possibili ipotesi ![]() come quella che ottimizza una regressione ai minimi quadrati pesata
come quella che ottimizza una regressione ai minimi quadrati pesata
Anche Gentle AdaBoost può essere usato con il Decision Stump.
In questo caso il minimo di (4.73) dell'algoritmo di decisione assume una forma notevole in
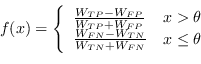 |
(4.74) |
Per motivi storici, AdaBoost non manifesta esplicitamente un formalismo statistico.
La prima cosa che si nota è che la risposta del classificatore di AdaBoost non è una probabilità, in quanto non limitata tra ![]() .
Oltre a questo problema, parzialmente risolto da Real AdaBoost, minimizzare la loss-function (4.53) non sembra un approccio statistico come lo potrebbe essere invece massimizzare la verosimiglianza.
È possibile tuttavia dimostrare che la funzione di costo di AdaBoost massimizza un funzione molto simile alla Bernoulli log-likelihood.
.
Oltre a questo problema, parzialmente risolto da Real AdaBoost, minimizzare la loss-function (4.53) non sembra un approccio statistico come lo potrebbe essere invece massimizzare la verosimiglianza.
È possibile tuttavia dimostrare che la funzione di costo di AdaBoost massimizza un funzione molto simile alla Bernoulli log-likelihood.
Per queste ragioni è possibile estendere AdaBoost alla teoria della regressione logistica, descritta in sezione 3.7.
La regressione logistica additiva assume la forma
Il problema diventa quello di trovare una loss function adeguata a questa rappresentazione, ovvero individuare una variante di AdaBoost che massimizza esattamente la Bernoulli log-likelihood (FHT00).
Massimizzare la verosimiglianza di (4.76) equivale a minimizzare la log-loss
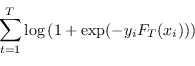 |
(4.77) |
LogitBoost per primo estende AdaBoost al problema dell'ottimizzazione logistica di una funzione ![]() sotto la funzione costo
sotto la funzione costo
![]() , massimizzando la Bernoulli log-likelihood usando iterazioni di tipo Newton.
, massimizzando la Bernoulli log-likelihood usando iterazioni di tipo Newton.
I pesi associati a ogni campione derivano direttamente dalla distribuzione di probabilità
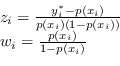 |
(4.78) |
Questo comportamento può essere rappresentato da una funzione costo del tipo
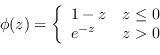 |
(4.79) |
Paolo medici