Next: AdaBoost e le sue Up: Ensemble Learning Previous: Alberi di Decisione
Uno dei classificatori Ensemble che ha attirato più interesse da parte dei ricercatori negli ultimi anni è sicuramente AdaBoost (FS95). L'idea base di AdaBoost è quella di costruire una lista di classificatori assegnando, in maniera iterativa, un peso ad ogni nuovo classificatore considerando la sua capacità di riconoscere campioni non correttamente identificati dagli altri classificatori già coinvolti nell'addestramento. Tutti questi classificatori coinvolti voteranno con il peso loro assegnato e la scelta finale avverà per maggioranza.
Le tecniche di Boosting permettono di generare un classificatore nella forma di modello additivo:
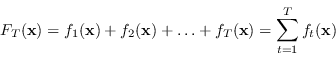 |
(4.52) |
Esaminiamo il caso di classificazione binaria, e sia
![]() l'insieme degli
l'insieme degli ![]() campioni disponibili per l'addestramento.
campioni disponibili per l'addestramento.
Una scelta abbastanza diffusa nell'ambito di fitting di modelli è quella di usare la regressione ai minimi quadrati (metrica ottima in caso di rumore gaussiano per esempio) per ottenere il modello additivo
![]() , minimizzando la quantità
, minimizzando la quantità
![]() .
Tuttavia, a seguito di numerosi esperimenti, si è visto che la funzione costo quadratica non è la scelta ottima nei problemi di classificazione.
.
Tuttavia, a seguito di numerosi esperimenti, si è visto che la funzione costo quadratica non è la scelta ottima nei problemi di classificazione.
L'approccio di AdaBoost suggerisce invece che l'unione di tutti questi classificatori minimizzi una funzione costo differente, migliore, ovvero la funzione di perdita esponenziale (exponential loss):
Siccome la minimizzazione globale della funzione (4.53) solitamente è impossibile, si può procedere in due modi
Sotto queste considerazioni l'obiettivo del processo di addestramento si riduce a individuare un classificatore addizionale ![]() che minimizzi di volta in volta la quantità
che minimizzi di volta in volta la quantità
AdaBoost è una tecnica che risponde a tutte queste esigenze.
Si supponga pertanto di avere a disposizione
![]() classificatori binari, ognuno dei quali, valutando la caratteristica
classificatori binari, ognuno dei quali, valutando la caratteristica ![]() , con
, con
![]() , restituisca una opinione
, restituisca una opinione ![]() .
.
Sia la funzione
![]() , definita come
, definita come
L'obiettivo è ottenere un classificatore forte
![]() come somma lineare pesata dei classificatori
come somma lineare pesata dei classificatori ![]() , il cui segno determini l'ipotesi globale:
, il cui segno determini l'ipotesi globale:
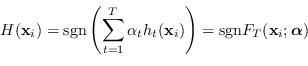 |
(4.56) |
Per permettere di assegnare un voto al classificatore, è necessario che a ogni campione in ingresso ![]() sia assegnato un certo peso
sia assegnato un certo peso ![]() : più il peso è alto più il campione è stato classificato in maniera non corretta fino a questo punto dell'addestramento mentre più il peso è basso più è stato classificato correttamente.
Alla prima iterazione, tutti i pesi sono posti uguali, pari a
: più il peso è alto più il campione è stato classificato in maniera non corretta fino a questo punto dell'addestramento mentre più il peso è basso più è stato classificato correttamente.
Alla prima iterazione, tutti i pesi sono posti uguali, pari a ![]() , in modo da avere una esatta distribuzione statistica.
Varianti come l'Asymmetric AdaBoost assegnano pesi differenti alle diverse categorie coinvolte.
, in modo da avere una esatta distribuzione statistica.
Varianti come l'Asymmetric AdaBoost assegnano pesi differenti alle diverse categorie coinvolte.
Sia
![]() la funzione che esprime il successo (
la funzione che esprime il successo (![]() ) o il fallimento (
) o il fallimento (![]() ) del classificatore
) del classificatore ![]() a valutare il campione
a valutare il campione ![]() .
Dati i pesi associati a ogni campione, è possibile per ogni classificatore calcolare
.
Dati i pesi associati a ogni campione, è possibile per ogni classificatore calcolare ![]() , la somma dei pesi associati gli insuccessi, e
, la somma dei pesi associati gli insuccessi, e ![]() , la somma dei pesi associati alle classificazioni corrette, ovvero attraverso la definizione di
, la somma dei pesi associati alle classificazioni corrette, ovvero attraverso la definizione di ![]() , in forma compatta
, in forma compatta
Sia ![]() la misura dell'errore del classificatore
la misura dell'errore del classificatore ![]() calcolata come
calcolata come
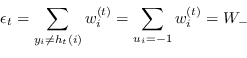 |
(4.58) |
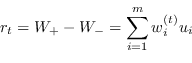 |
(4.59) |
Le iterazioni dell'algoritmo di AdaBoost sono le seguenti:
Il parametro di normalizzazione ![]() vale
vale
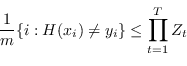 |
(4.62) |
La scelta ottima di ![]() (e di riflesso quella di
(e di riflesso quella di ![]() ) è quella dove la funzione (4.61) assume il minimo, ovvero
) è quella dove la funzione (4.61) assume il minimo, ovvero
Scegliendo come peso quello di equazione (4.63) che minimizza ![]() , dopo ogni iterazione di AdaBoost i pesi associati a campioni identificati correttamente vengono diminuiti di un fattore
, dopo ogni iterazione di AdaBoost i pesi associati a campioni identificati correttamente vengono diminuiti di un fattore
![]() ovvero
ovvero
![]() , mentre i pesi associati a campioni valutati erroneamente dall'ipotesi
, mentre i pesi associati a campioni valutati erroneamente dall'ipotesi ![]() vengono aumentati di un fattore
vengono aumentati di un fattore
![]() ovvero
ovvero
![]() .
.
Questo algoritmo è quello che viene definito in letteratura AdaBoost.M1 o Discrete AdaBoost (FHT00).
Le ipotesi
![]() usate da AdaBoost sono feature che possono assumere i soli valori
usate da AdaBoost sono feature che possono assumere i soli valori ![]() .
.
Il funzionamento intuitivo di AdaBoost è molto semplice: AdaBoost per ogni nuovo classificatore aggiunto alla serie si concentra sui pattern in ingresso che finora sono stati classificati peggio.
AdaBoost ha diverse interpretazioni: come classificatore che massimizza il margine, regressione logistica a un modello additivo, come minimizzatore a discesa del gradiente a passi discreti ma anche come regressione con tecnica di Newton.
AdaBoost, come SVM, ottiene come risultato quello di massimizzare il margine di separazione tra le classi, anche se con metriche differenti. In questo modo, entrambi, riescono ad essere meno sensibile a problemi come l'overfitting.
Paolo medici