Next: ADAptive BOOSTing Up: Ensemble Learning Previous: Ensemble Learning
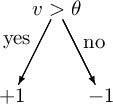 |
Un Albero di Decisione (Decision Tree) è un metodo molto semplice ed efficace per realizzare un classificatore e l'addestramento degli alberi di decisione è una delle tecniche attuali di maggior successo. Un albero di decisione è un albero di classificatori (Decision Stump) dove ogni nodo interno è associato ad una particolare “domanda” su una caratteristica (feature). Da questo nodo dipartono tanti archi quanti sono i possibili valori che la caratteristica può assumere, fino a raggiungere le foglie che indicano la categoria associata alla decisione. Particolare attenzione normalmente è posta per i nodi di decisione binaria.
Una buona “domanda” divide i campioni di classi eterogenee in dei sottoinsiemi con etichette abbastanza omogenee, stratificando i dati in modo da mettere poca varianza in ogni strato.
Per permettere questo è necessario definire una metrica che misuri questa impurità.
Definiamo ![]() come un sottoinsieme di campioni di un particolare insieme di addestramento formato da
come un sottoinsieme di campioni di un particolare insieme di addestramento formato da ![]() possibili classi.
possibili classi.
![]() è di fatto una variabile aleatoria, che assume solo valori discreti (il caso continuo è comunque uguale).
È possibile associare ad ogni valore discreto
è di fatto una variabile aleatoria, che assume solo valori discreti (il caso continuo è comunque uguale).
È possibile associare ad ogni valore discreto ![]() , che può assumere
, che può assumere ![]() , la distribuzione di probabilità
, la distribuzione di probabilità ![]() .
.
![]() è un data set formato da
è un data set formato da ![]() classi e
classi e ![]() è la frequenza relativa della classe
è la frequenza relativa della classe ![]() all'interno dell'insieme
all'interno dell'insieme ![]() .
.
 |
Data la definizione di ![]() , negli alberi di decisione sono largamente usate le seguenti metriche:
, negli alberi di decisione sono largamente usate le seguenti metriche:
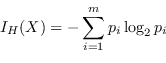 |
(4.46) |
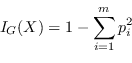 |
(4.47) |
| (4.48) |
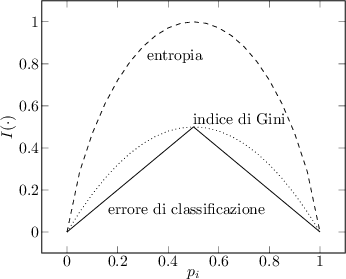
Intuitivamente un nodo con distribuzione delle classi ![]() ha impurità minima, mentre un nodo con distribuzione uniforme
ha impurità minima, mentre un nodo con distribuzione uniforme ![]() ha impurità massima.
ha impurità massima.
Una “domanda” ![]() , che ha
, che ha ![]() possibili risposte, divide l'insieme
possibili risposte, divide l'insieme ![]() nei sottoinsiemi
nei sottoinsiemi
![]() .
.
Per testare quanto bene la condizione viene eseguita, bisogna confrontare il grado di impurità dei nodi figli con l'impurità del nodo padre: maggiore è la loro differenza, migliore è la condizione scelta.
Data una metrica ![]() che misuri l'impurità, il guadagno
che misuri l'impurità, il guadagno ![]() è un criterio che può essere usato per determinare la bontà della divisione:
è un criterio che può essere usato per determinare la bontà della divisione:
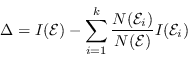 |
(4.49) |
Se viene usata come metrica l'entropia, il guadagno ![]() è conosciuto come Information Gain (TSK06).
è conosciuto come Information Gain (TSK06).
Gli alberi di decisione inducono algoritmi che scelgono una condizione di test che massimizza il guadagno ![]() .
Siccome
.
Siccome
![]() è uguale per tutti i possibili classificatori e
è uguale per tutti i possibili classificatori e
![]() è costante, massimizzare il guadagno è equivalente a minimizzare la somma pesata delle impurità dei nodi figli:
è costante, massimizzare il guadagno è equivalente a minimizzare la somma pesata delle impurità dei nodi figli:
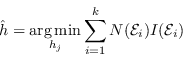 |
(4.50) |
Nel caso di classificatori binari, la metrica di Gini è ampiamente utilizzata, in quando il guadagno da minimizzare si riduce a
| (4.51) |
Gli alberi di decisione si adattano sia molto bene che velocemente ai dati di addestramento e conseguentemente, se non limitati, soffrono in maniera sistematica del problema di overfitting. Normalmente agli alberi viene applicato un algoritmo di raffinamento (pruning) per ridurre, ove possibile, il problema di overfitting. Gli approcci di pruning sono solitamente due: pre-pruning o post-pruning. Il pre-pruning si limita a fermare la creazione dell'albero sotto determinate condizioni per evitare una eccessiva specializzazione (esempio massima dimensione dell'albero). Il post-pruning invece raffina un albero già creato, eliminando quei rami che non soddisfano alcune condizioni su un validation set precedentemente selezionato.
Questa tecnica di creazione di un albero di decisione viene solitamente indicata come Classification and regression trees (CART) (B$^+$84). Infatti, nel caso reale in cui le caratteristiche analizzate sono grandezze statistiche, non si parla di creare un albero di classificazione, ma più propriamente di costruire un albero di regressione. Trovare la partizione ottima dei dati è un problema NP-completo, perciò normalmente si fa uso di algoritmi ingordi greedy come quello mostrato in sezione.
Paolo medici