Regressione Logistica

Figura 3.2: Funzione Logistica

Esiste una famiglia di modelli lineari, che mettono in relazione la variabile dipendente con le variabili esplicative attraverso una funzione non lineare, chiamati modelli lineari generalizzati (generalized linear model). La regressione logistica si situa in questa classe di modelli, nel caso particolare in cui la variabile $y$ sia dicotomica, ovvero possa assumere solo valori $0$ o $1$. Per sua natura, questo genere di problemi, assume una notevole importanza nei problemi di classificazione.

Nel caso di problemi binari è possibile definire la probabilità di successo e insuccesso

$$\begin{array}{l} P[Y=1\vert\mathbf{x}]=p(\mathbf{x}) \\ P[Y=0\vert\mathbf{x}]=1-p(\mathbf{x}) \\ \end{array}$$ (3.101)

La risposta di un predittore lineare del tipo

$$y' = \boldsymbol\beta \cdot \mathbf{x} + \varepsilon$$ (3.102)

non è limitata tra $0$ e $1$ perciò non è adatta a questo scopo. Risulta necessario associare la risposta del predittore lineare con la risposta di una certa funzione $g$, funzione della probabilità $p(\mathbf{x})$

$$g(p(\mathbf{x}) ) = \boldsymbol\beta \cdot \mathbf{x} + b$$ (3.103)

dove $g(p)$, mean function, è una funzione non lineare definita tra $[0,1]$. $g(p)$ deve essere invertibile e l'inversa $g^{-1}(y')$ è la link function.

Un modello ampiamente usato per la funzione $g(p)$ è la funzione logit definita come:

$$logit(p) = \log \frac{p}{1-p} = \boldsymbol\beta \cdot \mathbf{x}$$ (3.104)

La funzione $\frac{p}{1-p}$, siccome rappresenta quante volte il successo è maggiore dell'insuccesso, è detta odds-ratio e di conseguenza la funzione (3.104) rappresenta il logaritmo della probabilità che accada un evento rispetto alla probabilità che il medesimo evento non accada (log-odds).

La sua funzione inversa esiste e vale

$$\E[Y\vert\mathbf{x}] = p( \mathbf{x} ) = \frac{ e^{\boldsymb... ...dot \mathbf{x}} }{ 1 + e^{\boldsymbol\beta \cdot \mathbf{x}} }$$ (3.105)

`ed è la funzione logistica.

Il metodo della massima verosimiglianza in questo caso non coincide con il metodo dei minimi quadrati ma con

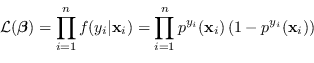$$\mathcal{L}(\boldsymbol\beta) = \prod_{i=1}^{n} f(y_i\vert \... ...y_i} ( \mathbf{x}_i) \left(1 - p^{y_i} ( \mathbf{x}_i) \right)$$ (3.106)

da cui la funzione di verosimiglianza logaritmica

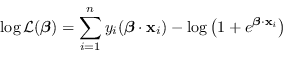$$\log \mathcal{L}(\boldsymbol\beta) = \sum_{i=1}^{n} y_i (\bo... ...log \left( 1 + e^{\boldsymbol\beta \cdot \mathbf{x}_i} \right)$$ (3.107)

la cui massimizzazione, attraverso tecniche iterative, permette la stima dei parametri $\boldsymbol\beta$.