Metodi di Regressione e Ottimizzazione per l'Analisi di Modelli

Uno dei problemi più diffusi all'interno della visione artificiale (e in generale all'interno della teoria dell'informazione) è quello di far adattare un insieme di misure affette da rumore (per esempio i pixel di un'immagine) a un modello predefinito.

Oltre alla presenza di rumore, che potrebbe essere sia gaussiano bianco ma potenzialmente di qualunque distribuzione statistica, c'è da considerare il problema dell'eventuale presenza di outlier, termine utilizzato in statistica per indicare dati troppo distanti dal modello per farne effettivamente parte.

In questo capitolo vengono presentate sia diverse tecniche regressive volte a ricavare i parametri 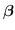$\boldsymbol\beta$ di un modello stazionario dato un insieme di dati affetti da rumore sia tecniche per individuare e rimuovere gli outlier dai dati in ingresso.

Nel capitolo successivo verranno presentate invece tecniche di “regressione” più legate al tema della classificazione.

Per stimare i parametri di un modello alcune tecniche presenti in letteratura sono le seguenti:

Least Squares Fitting

Se i dati sono tutti inliers, non ci sono outliers e l'unico disturbo è rumore additivo gaussiano bianco, la regressione ai minimi quadrati è la tecnica ottima (sezione 3.2);

M-Estimator

La presenza anche di pochi outlier sposta di molto il modello in quanto gli errori vengono pesati al quadrato (Hub96): pesare in maniera non quadratica i punti lontani del modello stimato produce miglioramenti nella stima stessa (sezione 3.8);

IRLS

iteratively reweighted least squares viene usata quando gli outliers sono molto distanti dal modello e in bassa quantità: in questa condizione si può eseguire una regressione iterativa (sezione 3.9), dove a ogni ciclo i punti con errore troppo elevato vengono rimossi (ILS) o pesati in maniera differente (IRLS);

Hough

Se i dati in ingresso sono sia affetti da errore che da molti outliers e potenzialmente c'è presenza di una distribuzione multimodale, ma con il modello formato da pochi parametri, la trasformata di Hough (Hou59) permette di ottenere il modello più diffuso dal punto di vista statistico (sezione 3.11);

RANSAC

Se gli outliers sono comparabili in numero con gli inliers e il rumore è molto basso (rispetto alla posizione degli outliers), il RANdom SAmpling and Consensus (FB87) permette di ottenere il miglior modello presente sulla scena (sezione 3.12);

LMedS

Il Least Median of Squares è un algoritmo, simile a RANSAC, che ordina i punti in base alla distanza del modello generato casualmente e sceglie fra tutti il modello con mediana dell'errore minore (Rou84) (sezione 3.12.2);

Kalman

È possibile infine usare un filtro di Kalman per ricavare i parametri di un modello (vedi 2.12.9) quando tale informazione è richiesta a tempo di esecuzione.

Solamente RANSAC e la Trasformata di Hough permettono di gestire ottimamente il caso in cui nella misura siano presenti due o più distribuzioni che contemporaneamente si avvicinano al modello.

Nulla infine impedisce di usare tecniche miste, per esempio un Hough abbastanza grossolano (pertanto veloce e con basso impatto in termini di memoria) per rimuovere gli outliers e successivamente una regressione ai minimi quadrati per ottenere i parametri del modello in maniera più precisa.