Next: Regressione Logistica Up: Regressioni notevoli Previous: Regressione ad un ellisse
È chiaramente possibile generalizzare la regressione della parabola, della circonferenza e dell'ellissi a una qualsiasi conica (sezione 1.6) arbitrariamente orientata.
Siano
![]() , con
, con
![]() , punti affetti da rumore appartenenti al luogo dei punti da stimare.
, punti affetti da rumore appartenenti al luogo dei punti da stimare.
L'equazione (1.56) può essere riscritta nella forma
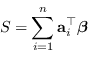 |
(3.99) |
Una formulazione alternativa per ricavare i parametri delle coniche si può trovare in (FPF99).
Infine, per capire se un punto è vicino all'equazione di una conica ovvero per ottenere una approssimazione geometrica della distanza punto-conica, si può calcolare l'errore di Sampson (sezione 3.3.7) sfruttando il fatto che, per una conica di equazione (1.56), il gradiente della varietà assume una forma molto semplice da calcolare:
| (3.100) |
Paolo medici