Regressione ad un ellisse

Come per il cerchio è possibile eseguire sia una minimizzazione algebrica, che geometrica.

L'equazione quadratica di un ellisse è

$$f(\mathbf{x}) = \mathbf{x}^\top \mathbf{A} \mathbf{x} + \mathbf{b}^{\top} \mathbf{x} + c = 0$$ (3.96)

dove $\mathbf{A}$ è una matrice simmetrica, definita positiva. Anche in questo caso la soluzione del problema omogeneo (3.96) permette di ricavare le 6 incognite (conosciute a meno di un fattore moltiplicativo) del sistema.

La soluzione non lineare che minimizza la quantità geometrica si può ottenere usando la rappresentazione parametrica dell'ellisse

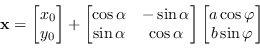$$\mathbf{x} = \begin{bmatrix} x_0 \\ y_0 \end{bmatrix} ... ...{bmatrix} a \cos \varphi \\ b \sin \varphi \end{bmatrix}$$ (3.97)

dove $(x_0,y_0)$ rappresenta il centro dell'ellissi, $(a,b)$ la lunghezza dei due semiassi e $\alpha$ la rotazione dell'ellissi rispetto al centro. Come per il cerchio, le $\varphi_i$ saranno variabili sussidiarie e il problema non lineare diventa di $5+n$ incognite con $2n$ equazioni.