Next: Discesa del Gradiente Up: Metodi di ottimizzazione Previous: Metodi di ottimizzazione
Il problema di trovare i minimi di una funzione può essere ricondotto al problema di trovare gli zeri di una funzione, nel caso specifico la derivata prima della funzione costo ![]() .
.
Sia pertanto
![]() una funzione multivariata derivabile di cui sia richiesto di trovare
una funzione multivariata derivabile di cui sia richiesto di trovare
L'obiettivo è modificare il valore di ![]() di un valore
di un valore
![]() in maniera tale che la funzione costo calcolata in
in maniera tale che la funzione costo calcolata in
![]() sia esattamente zero.
Ignorando i contributi di ordine di ordine superiore a
sia esattamente zero.
Ignorando i contributi di ordine di ordine superiore a
![]() , la stima del
, la stima del
![]() che in prima approssimazione fa avvicinare a zero la funzione
che in prima approssimazione fa avvicinare a zero la funzione ![]() è la soluzione del sistema lineare (3.30) con la condizione (3.29), ovvero
è la soluzione del sistema lineare (3.30) con la condizione (3.29), ovvero
| (3.32) |
Nel caso di singola variabile ![]() il metodo di Newton si riduce a
il metodo di Newton si riduce a
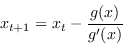 |
(3.33) |
In calcolo numerico questo è il cosiddetto metodo di Newton (o di Newton-Raphson) per trovare gli zeri di una funzione.
I punti di massimo e minimo di una funzione sono i punti per i quali si riesce ad annullare il gradiente.
Si può pertanto applicare questa tecnica per trovare i massimi e minimi di una funzione
![]() definendo
definendo
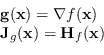 |
(3.34) |
Ora, nel caso specifico dei metodi di ottimizzazione, la funzione ![]() è la funzione costo
è la funzione costo
![]() .
Pertanto, quando la matrice Hessiana di
.
Pertanto, quando la matrice Hessiana di
![]() è non singolare, si ottiene l'equazione di variazione dei parametri
è non singolare, si ottiene l'equazione di variazione dei parametri
Paolo medici