Next: Autovalori e Autovettori Up: Elementi Previous: Elementi
Analizzando sistemi reali è facile imbattersi nel problema di dover ricavare la “soluzione” di un sistema lineare sovradimensionato.
L'importanza di questo argomento è evidente: quando si eseguono osservazioni su un sistema reale questo risulta naturalmente affetto da rumore, appunto, di osservazione. Questo rumore chiaramente compromette il risultato della singola osservazione ma, fortunatamente, è normalmente possibile acquisire molte più osservazioni che incognite ottenendo cosı un sistema sovradimensionato. In queste condizioni, per ottenere una soluzione al problema che minimizzi l'errore, è richiesto l'utilizzo di una tecnica di regressione numerica, per esempio, ai minimi quadrati. In questa prima sezione sono presentate tecniche matematiche ampiamente utilizzate in tutto il libro: per ulteriori dettagli riguardo queste tecniche si può fare riferimento al capitolo 3 incentrato totalmente su questo argomento.
Si abbia pertanto un sistema lineare sovradimensionato (overdetermined)
Definiamo1.1 come metrica dell'errore il modulo del residuo
Se si moltiplica l'equazione (1.1) per
![]() si ottiene un sistema lineare “tradizionale” che ammette come soluzione
si ottiene un sistema lineare “tradizionale” che ammette come soluzione
Se il sistema è ben condizionato, la tecnica più stabile per risolvere un problema alle normal equations è la fattorizzazione di Cholesky.
Si può dimostrare che una soluzione ![]() , meglio condizionata e che minimizza la funzione (1.2), esiste e vale:
, meglio condizionata e che minimizza la funzione (1.2), esiste e vale:
Per costruzione ![]() è una soluzione del sistema (1.1) ed è anche il vettore che minimizza la funzione (1.2).
Viene indicata con
è una soluzione del sistema (1.1) ed è anche il vettore che minimizza la funzione (1.2).
Viene indicata con
![]() la matrice pseudoinversa (pseudoinverse matrix) di
la matrice pseudoinversa (pseudoinverse matrix) di ![]() e vale
e vale
Questa soluzione del sistema è detta pseudoinversa di Moore-Penrose.
La pseudoinversa ha le seguenti proprietà
È necessario precisare fin da subito che nel minimizzare la quantità (1.2) non si è fatta nessuna ipotesi sulla distribuzione del rumore all'interno delle varie componenti di cui la matrice è composta: senza tale informazione non c'è garanzia che la soluzione sarà ottima dal punto di vista statistico. Senza ipotesi sulla distribuzione del rumore, la soluzione ottenuta con questa minimizzazione è infatti una soluzione puramente algebrica che minimizza appunto un errore algebrico (algebraic error).
È possibile ottenere una soluzione leggermente migliore dal punto di vista statistico quando il rumore è gaussiano bianco a media nulla e si conosce il valore della varianza del rumore su ogni osservazione. In questo caso è possibile assegnare ad ogni equazione del sistema pesi differenti, moltiplicando ogni riga del sistema per un opportuno peso in modo da pesare in maniera differente ogni dato acquisito. Discussione più approfondita su questo argomento si trova in sezione 3.2 e in generale nel capitolo 2 si affronterà il caso generale dove si conosce il modo con cui l'errore sui dati osservati incide sulla stima dei parametri.
Esistono invece delle tecniche stabili basate su fattorizzazioni che permettono di ricavare la soluzione partendo direttamente dalla matrice ![]() .
.
Usando per esempio la fattorizzazione QR, algoritmo notoriamente stabile dal punto di vista numerico, della matrice ![]() il problema originale (1.1) si trasforma nel problema
il problema originale (1.1) si trasforma nel problema
![]() e la soluzione si può ricavare da
e la soluzione si può ricavare da
![]() , sfruttando l'ortogonalità della matrice
, sfruttando l'ortogonalità della matrice ![]() .
Nella fattorizzazione QR vige la relazione
.
Nella fattorizzazione QR vige la relazione
![]() ovvero
ovvero ![]() è fattorizzazione di Cholesky di
è fattorizzazione di Cholesky di
![]() : attraverso questa relazione si può ricavare infine la pseudoinversa in maniera esplicita.
: attraverso questa relazione si può ricavare infine la pseudoinversa in maniera esplicita.
Attraverso invece la Decomposizione ai Valori Singolari Singular Value Decomposition (SVD), la matrice sovradimensionata ![]() viene scomposta in 3 matrici dalle proprietà interessanti.
Sia
viene scomposta in 3 matrici dalle proprietà interessanti.
Sia
![]() la decomposizione ai valori singolari (SVD) di
la decomposizione ai valori singolari (SVD) di ![]() .
.
![]() è una matrice unitaria di dimensioni
è una matrice unitaria di dimensioni ![]() (a seconda del formalismo usato, complete SVD o economic SVD, le dimensioni delle matrici possono cambiare, e
(a seconda del formalismo usato, complete SVD o economic SVD, le dimensioni delle matrici possono cambiare, e ![]() diventare
diventare ![]() ),
), ![]() è una matrice diagonale che contiene i valori singolari (gli autovalori della matrice
è una matrice diagonale che contiene i valori singolari (gli autovalori della matrice
![]() , di dimensioni, a seconda del formalismo,
, di dimensioni, a seconda del formalismo, ![]() o
o ![]() ) e
) e
![]() è una matrice ortonormale, trasposta coniugata, di dimensioni
è una matrice ortonormale, trasposta coniugata, di dimensioni ![]() .
.
Attraverso un procedimento puramente matematico si ottiene che la pseudoinversa di ![]() equivale a
equivale a
Riassumendo, i modi per risolvere un sistema lineare sovradimensionato sono
Dettagli ulteriori sulla pseudoinversa di Moore-Penrose possono essere trovati in molti libri, per esempio in (CM09) o nel testo fondamentale di calcolo numerico (GVL96).
Esaminiamo ora il caso in cui il sistema lineare da risolvere sia invece omogeneo.
Un sistema lineare omogeneo ha la forma
| (1.8) |
Anche in questo caso la SVD si dimostra una tecnica estremamente efficace e computazionalmente stabile: le basi del kernel di ![]() infatti sono esattamente le colonne di
infatti sono esattamente le colonne di ![]() associate ai valori singolari (autovalori) nulli della matrice diagonale
associate ai valori singolari (autovalori) nulli della matrice diagonale ![]() .
In genere, a causa della presenza di rumore, non esisterà un valore singolare esattamente nullo ma deve essere scelta la colonna associata al minimo valore singolare.
.
In genere, a causa della presenza di rumore, non esisterà un valore singolare esattamente nullo ma deve essere scelta la colonna associata al minimo valore singolare.
Gli autovettori associati a valori singolari nulli della matrice ![]() rappresentano pertanto il kernel della matrice stessa e il numero di autovalori nulli rappresenta la dimensione del kernel stesso.
Va notato come nell'equazione (1.6) la presenza di zeri nella matrice diagonale
rappresentano pertanto il kernel della matrice stessa e il numero di autovalori nulli rappresenta la dimensione del kernel stesso.
Va notato come nell'equazione (1.6) la presenza di zeri nella matrice diagonale ![]() fosse problematica: ora si capisce che tale presenza è sintomo del fatto che una delle componenti del problema è totalmente incorrelata con la soluzione e, in quanto tale, potrebbe essere trascurata:
tale risultato infatti sarà utilizzato nella sezione 2.10.1 nella trattazione dell'agoritmo PCA.
fosse problematica: ora si capisce che tale presenza è sintomo del fatto che una delle componenti del problema è totalmente incorrelata con la soluzione e, in quanto tale, potrebbe essere trascurata:
tale risultato infatti sarà utilizzato nella sezione 2.10.1 nella trattazione dell'agoritmo PCA.
La soluzione del sottospazio di ![]() è pertanto
è pertanto
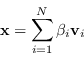 |
(1.9) |
La decomposizione SVD risulta una delle tecniche più stabili e versatili sviluppata negli ultimi anni per la risoluzione di sistemi lineari e, in tutto questo libro, si farà larghissimo uso di tale tecnologia.