Condizionamento nei sistemi lineari sovradimensionati

Nella sezione 2.6 e seguenti si è discusso di come il rumore si propaghi attraverso trasformazioni lineare e non lineari.

In questa sezione invece si studia il caso complementare dove è conosciuta la stima del rumore sulla variabile in uscita dal sistema lineare mentre si vuole sapere la stima del rumore sulle variabili in ingresso ovvero la bontà con cui si è ottenuta la soluzione di un sistema lineare. Per buona parte di questa sezione si fa riferimento alla teoria discussa in sezione 1.1 e ne è di fatto la continuazione, per integrarla poi, con nella sezione 3.5 al discorso più generale di regressione a modelli non lineari.

Sia pertanto

$$\mathbf{A} \mathbf{x} = \mathbf{b}$$ (2.46)

un sistema lineare, ideale ovvero non affetto da rumore, con $\mathbf {x}$ la soluzione esatta del problema.

Una perturbazione $\delta \mathbf{b}$ sulla colonna dei termini noti (osservazioni,uscite), in

$$\mathbf{A} \mathbf{x} = \tilde{\mathbf{b}}$$ (2.47)

con $\tilde{\mathbf{b}} = \mathbf{b} + \delta \mathbf{b}$, provoca una perturbazione $\tilde{\mathbf{x}} = \mathbf{x} + \delta \mathbf{x}$ sulla soluzione di entità pari a

$$\delta \mathbf{x} = \mathbf{A}^{-1} \delta \mathbf{b}$$ (2.48)

In questo modo si ricade nel caso visto in precedenza di propagazione di rumore in un sistema lineare.

Un indice interessante consiste nel calcolare la norma dell'errore in relazione al valore atteso. Tale relazione vale

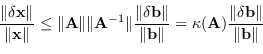$$\frac{\Vert \delta \mathbf{x} \Vert}{\Vert \mathbf{x} \Vert... ...) \frac{\Vert \delta \mathbf{b} \Vert}{\Vert \mathbf{b} \Vert}$$ (2.49)

avendo definito $\kappa(\mathbf{A})$ numero di condizionamento (condition number) della matrice dei coefficienti (sensitivity matrix) $\mathbf{A}$. Nel caso particolare in cui $\mathbf{A}$ sia singolare, il condizionamento della matrice si pone pari a $\kappa(\mathbf{A})=\infty$.

Estendiamo ora l'analisi al caso in cui il sistema sia un sistema lineare sovradimensionato. A questo scopo è possibile ricavare il condizionamento di una matrice usando un'ulteriore proprietà della decomposizione SVD. Sia

$$\mathbf{x} = \mathbf{V} \mathbf{S}^{-1} \mathbf{U}^{*} \mathbf{b}$$ (2.50)

la soluzione di un problema lineare sovradimensionato attraverso il metodo della decomposizione SVD. Se si esplicita l'equazione (2.50), si può mostrare come la soluzione di un sistema lineare, soluzione ottenuta attraverso la decomposizione SVD, ha come forma

$$\mathbf{x}=\sum \frac{ \mathbf{u}^{\top}_i \mathbf{b} } {\sigma_i} \mathbf{v}_i$$ (2.51)

Da questa formulazione si vede che, quando i valori singolari $\sigma_i$ sono bassi, ogni piccola variazione al numeratore viene amplificata: sotto la norma euclidea il numero di condizionamento di una matrice è esattamente il rapporto tra il più grande valore singolare rispetto al più piccolo. Il condizionamento è sempre positivo e un condizionamento prossimo all'unità indica una matrice ben condizionata.

Riassumendo il condizionamento ha le seguenti importanti proprietà:

• $\kappa(\mathbf{A}) = \kappa(\mathbf{A}^{-1})$
• $\kappa(c \mathbf{A}) = \kappa(\mathbf{A})$ per ogni $c \neq 0$
• $\kappa(\mathbf{A}) \geq 1$
• $\kappa(\mathbf{A}) = \frac{\sigma_1}{\sigma_n}$ se la norma è euclidea
• $\kappa(\mathbf{A}) = 1$ se $\mathbf{A}$ è ortogonale

Come è stato fatto notare nella sezione 1.1, la soluzione alle equazioni perpendicolari tende invece ad amplificare gli errori rispetto a soluzioni alternative. È facile dimostrare infatti che in questo caso

$$\kappa \left(\mathbf{A}^{\top}\mathbf{A} \right) = \left( \frac{\sigma_1}{\sigma^{n}} \right)^{2}$$ (2.52)