Next: Regressioni notevoli Up: Metodi di Regressione e Previous: Programmazione Quadratica (QP)
Trascurando la presenza di outlier nei dati in ingresso su cui eseguire la regressione, rimangono come importanti questioni aperte sia quella di dare un giudizio su quanto è buono il modello ottenuto e allo stesso tempo fornire un indice su quanto tale stima sia distante dal modello vero, a causa degli errori sui dati in ingresso.
In questa sezione viene trattato ampiamente il caso non-lineare: il caso lineare è equivalente usando al posto dello Jacobiano ![]() la matrice dei parametri
la matrice dei parametri ![]() in parte già affrontato in sezione 2.7.
in parte già affrontato in sezione 2.7.
Sia
![]() un vettore di realizzazioni di variabili aleatorie statisticamente indipendenti
un vettore di realizzazioni di variabili aleatorie statisticamente indipendenti
![]() e
e
![]() parametri del modello.
Uno stimatore intuitivo della bontà del modello è il root-mean-squared residual error (RMSE), chiamato anche standard error of the regression:
parametri del modello.
Uno stimatore intuitivo della bontà del modello è il root-mean-squared residual error (RMSE), chiamato anche standard error of the regression:
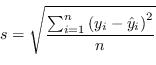 |
(3.67) |
Questo tuttavia non è un indice diretto della bontà della soluzione individuata ma solo quanto il modello trovato combacia con i dati in ingresso: si pensi ad esempio al caso limite dei sistemi non sovradimensionati dove il residuo sarà sempre zero, indipendentemente dalla quantità di rumore che agisce sulle singole osservazioni.
L'indice più adatto a stimare il modello è la matrice di varianza-covarianza dei parametri (Parameter Variances and Covariances matrix).
La propagazione in avanti della covarianza (covariance forward propagation) è stata già mostrata nella sezione 2.6 e, facendo un veloce rimando, esistono 3 metodi per eseguire tale operazione: `il primo è basato sulla approssimazione lineare del modello e coinvolge l'uso dello Jacobiano, il secondo è basato sulla più generica tecnica della simulazione Monte Carlo, e infine una via moderna alternativa, media tra le prime due, è la Unscent Transformation (sezione 2.12.5) che permette, empiricamente, stime fino al terzo ordine in caso di rumore gaussiano.
Il voler valutare la bontà dei parametri individuati
![]() data la covarianza del rumore stimata (Covariance Matrix Estimation) è esattamente il caso opposto perché richiede di calcolare la propagazione all'indietro della varianza (backward propagation).
Infatti, ottenuta tale matrice di covarianza, è possibile definire un intervallo di confidenza nell'intorno di
data la covarianza del rumore stimata (Covariance Matrix Estimation) è esattamente il caso opposto perché richiede di calcolare la propagazione all'indietro della varianza (backward propagation).
Infatti, ottenuta tale matrice di covarianza, è possibile definire un intervallo di confidenza nell'intorno di
![]() .
.
Tale bontà della stima dei parametri
![]() , nel caso non-lineare, può essere valutata in prima approssimazione attraverso l'inversione della versione linearizzata del modello (ma anche in questo caso tecniche come la Montecarlo o la UT possono essere utilizzate per stime più rigorose).
, nel caso non-lineare, può essere valutata in prima approssimazione attraverso l'inversione della versione linearizzata del modello (ma anche in questo caso tecniche come la Montecarlo o la UT possono essere utilizzate per stime più rigorose).
È possibile individuare la matrice di covarianza associata alla soluzione proposta
![]() nel caso in cui la funzione
nel caso in cui la funzione ![]() sia biunivoca e derivabile nell'intorno di tale soluzione.
Sia pertanto
sia biunivoca e derivabile nell'intorno di tale soluzione.
Sia pertanto
![]() funzione multivariata multidimensionale,
è possibile stimare il valor medio
funzione multivariata multidimensionale,
è possibile stimare il valor medio
![]() e la matrice di cross-covarianza
e la matrice di cross-covarianza
![]() dei residui allora la trasformazione inversa
dei residui allora la trasformazione inversa ![]() avrà valor medio
avrà valor medio
![]() e matrice di covarianza
e matrice di covarianza
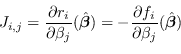 |
(3.69) |
Si noti che questo (l'inverso della matrice dell'informazione) è il limite inferiore di Cramer-Rao sulla covarianza che può avere uno stimatore corretto del parametro
![]() .
.
Nei casi in cui la trasformazione ![]() sia sottodeterminata, il rango dello Jacobiano
sia sottodeterminata, il rango dello Jacobiano ![]() , con
, con ![]() , è chiamato numero dei parametri essenziali (essential parameters).
In caso di trasformazione
, è chiamato numero dei parametri essenziali (essential parameters).
In caso di trasformazione ![]() sottodeterminata la formula (3.68) non è invertibile ma è possibile dimostrare che la migliore approssimazione della matrice di covarianza può essere ottenuta attraverso l'uso della pseudo-inversa:
sottodeterminata la formula (3.68) non è invertibile ma è possibile dimostrare che la migliore approssimazione della matrice di covarianza può essere ottenuta attraverso l'uso della pseudo-inversa:
Nel caso invece molto comune in cui ![]() sia una funzione scalare e il rumore di osservazione sia indipendente di varianza costante, la matrice di covarianza stimata asintoticamente (Asymptotic Covariance Matrix) si può scrivere in maniera più semplice come
sia una funzione scalare e il rumore di osservazione sia indipendente di varianza costante, la matrice di covarianza stimata asintoticamente (Asymptotic Covariance Matrix) si può scrivere in maniera più semplice come
| (3.70) |
La stima del rumore di osservazione può essere empirica, ipotizzando per la legge dei grandi numeri ![]() , calcolata attraverso
, calcolata attraverso
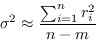 |
(3.71) |
Lo stimatore di covarianza di Eicker-White è leggermente differente e viene lasciato al lettore il suo studio.
La matrice di varianza-covarianza dei parametri rappresenta l'elissoide dell'errore.
Una metrica utile per dare un voto al problema è la configurazione D-ottima (D-optimal design):
| (3.72) |
| (3.73) |
Altre metriche sono per esempio la configurazione E-ottima (E-optimal design) che consiste nel massimizzare il minimo autovalore della matrice di Fisher ovvero minimizzare il più grande autovalore della matrice di varianza-covarianza. Geometricamente questo minimizza il massimo diametro dell'elissoide.
Paolo medici