Filtro di Kalman Sigma-Point

Un'alternativa nel caso non-lineare al filtro di Kalman Esteso è il filtro di Kalman a Punti Sigma. In risultati riportati da diversi esperimenti, nel caso di funzioni $f$ e $h$ non lineari, il Sigma Point Kalman Filter (SPKF) tende a fornire prestazioni migliori rispetto a EKF: la propagazione dell'errore linearizzata dal punto di vista statistico (SPKF) è generalmente migliore della propagazione dell'espansione in serie di Taylor (EKF).

Non solo lo stato, ma i diversi punti intorno la media (i sigma points) vengono propagati attraverso le funzioni che compongono l'aggiornamento e l'osservazione dello stato di Kalman. Il vantaggio di SPKF è quello di non richiedere il calcolo degli Jacobiani e normalmente permette una stima migliore di media e varianza del processo.

Il filtro di Kalman Unscented (Unscented Kalman filter) è una delle varie versioni del filtro di Kalman a Punti Sigma. In questo caso si fa uso della teoria per la propagazione dell'incertezza discussa in sezione 2.6.2 per stimare valor medio e covarianza dello stato a priori e dell'errore di osservazione.

Anche con il filtro Unscented è possibile gestire il caso in cui il rumore si inserisce nel sistema in maniera non additiva. Per generalizzare il caso di rumore non additivo definiamo, allo scopo di mantenere una sintassi uguale a quella discussa in sezione 2.6.2, una variabile chiamata stato aumentato $\mathbf{x}^{a} \in \mathbb{R}^{n^{a}}$ con $n^{a}=n+q$ formata dallo stato $\mathbf{x} \in \mathbb{R}^{n}$ e dal rumore di processo $w$, a media nulla, in modo da usare la funzione

$${\bm{\mathcal{X}}}^{-} = f(\mathbf{x}^{a}_{k-1}, \mathbf{u}_{k} )$$ (2.120)

di aggiornamento dello stato che permetta di tener conto in maniera non lineare e non additiva anche del contributo del rumore di processo. Allo stesso modo definiamo la matrice di covarianza aumentata come:

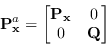$$\mathbf{P}_{\mathbf{x}}^{a} = \begin{bmatrix} \mathbf{P}_{\mathbf{x}} & 0 \\ 0 & \mathbf{Q} \end{bmatrix}$$ (2.121)

Nel caso in cui il rumore di processo sia additivo il sistema ridiventa simile a quello di Kalman lineare nella forma

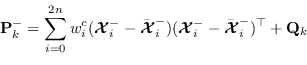$$\mathbf{P}^{-}_{k} = \sum_{i=0}^{2n} w^{c}_i ({\bm{\mathcal... ...{i} - \bar{{\bm{\mathcal{X}}}}^{-}_{i} )^{\top} + \mathbf{Q}_k$$ (2.122)

Dai sigma points ${\bm{\mathcal{X}}}^{-}_{i}$, proiettati attraverso $f$ e rappresentanti la distribuzione dello stato a priori, è possibile generare altri punti sigma in modo da ottenere la stima dell'osservazione a priori:

$${\bm{\mathcal{Z}}}_i = h({\bm{\mathcal{X}}}^{-}_{i})$$ (2.123)

con cui calcolare il valore più probabile dell'osservazione $\hat{\mathbf{z}}$ pesando i risultati ${\bm{\mathcal{Z}}}_i$ con i pesi dei sigma point associati come nell'equazione (2.44). Anche in questo caso il rumore di osservazione può essere inserito come stato aumentato o, se supposto additivo e indipendente, può venire sommato alla matrice di covarianza.

Attraverso la conoscenza dei punti sigma ${\bm{\mathcal{X}}}^{-}_{i}$ e ${\bm{\mathcal{Z}}}_i$ è possibile ottenere facilmente la covarianza $\cov (\bm{\mathcal{Z}})$ e anche la cross-covarianza $\cov (\bm{\mathcal{X}},\bm{\mathcal{Z}})$ generalizzando l'equazione (2.44):

$$\cov \left( \bm{\mathcal{X}},\bm{\mathcal{Z}}\right) \appro... ...bar{\mathbf{x}})(\bm{\mathcal{Z}}_i - \bar{\mathbf{z}})^{\top}$$ (2.124)

Data la conoscenza della covarianza $\cov (\bm{\mathcal{Z}})$ e la cross-covarianza $\cov (\bm{\mathcal{X}},\bm{\mathcal{Z}})$ il guadagno di Kalman sigma-point diventa esattamente come quello espresso dall'equazione (2.109) e l'aggiornamento della covarianza $\mathbf{P}_{k}$ segue l'equazione (2.110).