Next: Metodi Grid-based Up: Elementi di Statistica Previous: Elementi di probabilità
In questa sezione viene discusso il problema dei filtraggi statistici ovvero quella classe di problemi dove sono a disposizione dati proveniente da uno o più sensori affetti da rumore, dati che rappresentano l'osservazione dello stato dinamico di un sistema, non direttamente osservabile ma di cui è richiesta una stima. Il procedimento attraverso il quale si cerca di trovare la miglior stima dello stato interno di un sistema viene chiamato “filtraggio” in quanto è un metodo per filtrare via le diverse componenti di rumore. L'evoluzione di un sistema (l'evoluzione del suo stato interno) deve seguire leggi fisiche conosciute su cui va ad agire una componente di rumore (rumore di processo). È proprio attraverso la conoscenza delle equazioni che regolano l'evoluzione dello stato che è possibile fornire una stima migliore dello stato interno.
Un processo fisico può essere visto, nella sua rappresentazione di spazio di stato (State Space Model), attraverso una funzione che descrive come lo stato ![]() si evolve nel tempo:
si evolve nel tempo:
| (2.88) |
| (2.89) |
Questo formalismo è descritto nel dominio continuo del tempo.
Nelle applicazioni pratiche i segnali vengono campionati a tempo discreto ![]() e pertanto viene normalmente usata una versione a tempo discreto nella forma
e pertanto viene normalmente usata una versione a tempo discreto nella forma
Nei sistemi che soddisfano le equazioni (2.90), l'evoluzione dello stato è solo funzione dello stato precedente, mentre l'osservazione è solo funzione dello stato attuale (figura 2.4). Se un sistema soddisfa tali ipotesi si dice che il processo è markoviano: l'evoluzione del sistema e l'osservazione devono essere solo funzione dello stato corrente e non degli stati passati. L'accesso all'informazione sullo stato avviene sempre per via indiretta attraverso l'osservazione (Hidden Markov Model).
Molti approcci per stimare da un insieme di misure lo stato sconosciuto di un sistema non tengono conto della natura rumorosa di tali osservazioni. È possibile infatti costruire un algoritmo che esegua una regressione non lineare sulle osservazioni per ottenere la stima di tutti gli stati del problema, risolvendo un problema di ottimizzazione con un elevato numero di incognite.
I filtri, a differenza delle regressioni, si pongono come obiettivo quello di fornire la miglior stima di delle variabili (stato) man mano che i dati delle osservazioni arrivano. Dal punto di vista teorico le regressioni sono il caso ottimo, mentre i filtraggi convergono al risultato corretto solo dopo un numero di campioni sufficientemente elevato.
I filtri bayesiani si pongono come obiettivo quello di stimare all'istante di tempo ![]() , discreto, lo stato della variabile aleatoria
, discreto, lo stato della variabile aleatoria
![]() data un'osservazione del sistema, indiretta,
data un'osservazione del sistema, indiretta,
![]() .
.
Le tecniche di filtraggio permettono sia di ottenere la stima migliore dello stato sconosciuto ![]() ma anche la distribuzione di probabilità multivariata
ma anche la distribuzione di probabilità multivariata
![]() rappresentante la conoscenza che si ha dello stato stesso.
rappresentante la conoscenza che si ha dello stato stesso.
Data l'osservazione del sistema è possibile definire una densità di probabilità di ![]() a posteriori dell'osservazione dell'evento
a posteriori dell'osservazione dell'evento
![]() dovuta proprio alla conoscenza in più che si ottiene da tale osservazione:
dovuta proprio alla conoscenza in più che si ottiene da tale osservazione:
Applicando il teorema di Bayes all'equazione (2.91) si ottiene
| (2.92) |
Oltre alla conoscenza a posteriori della distribuzione di probabilità, è possibile sfruttare un'ulteriore informazione per migliorare la stima: la conoscenza a priori rispetto all'osservazione, ottenuta dal vincolo secondo il quale lo stato non si evolve in maniera totalmente imprevedibile ma viceversa può solo evolversi in determinati modi con determinate probabilità. Tali modi in cui il sistema si può evolvere sono funzione solamente dello stato corrente.
L'ipotesi di processo Markoviano implica infatti che l'unico stato passato che influisca sull'evoluzione del sistema sia quello di tempo ![]() , ovvero
, ovvero
![]() .
.
È pertanto possibile eseguire la predizione a priori, grazie all'equazione di Chapman-Kolmogorov:
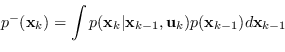 |
(2.93) |
Dalla conoscenza dello stato a priori e dall'osservazione ![]() è possibile riscrivere l'equazione (2.91) nell'equazione di aggiornamento dello stato
è possibile riscrivere l'equazione (2.91) nell'equazione di aggiornamento dello stato
Lo stato viene stimato alternando una fase di predizione (stima a priori) a una fase di osservazione (stima a posteriori). Questo processo, iterativo, prende il nome di stima bayesiana ricorsiva (Recursive Bayesian Estimation).
Le tecniche descritte in questa sezione faranno riferimento solo all'ultima osservazione disponibile per stimare lo stato. Dal punto di vista formale è possibile estendere la discussione al caso in cui vengano sfruttate tutte le osservazioni per ottenere una stima più accurata dello stato.
In questo caso le equazioni di filtraggio e predizione diventano
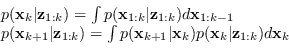 |
(2.95) |
In quanto stima di variabili continue, non risulta possibile sfruttare la teoria bayesiana “direttamente” ma sono state proposte in letteratura diversi approcci per permettere la stima in maniera efficiente sia dal punto di vista computazionale che di utilizzo della memoria.
A seconda che il problema sia lineare o non-lineare, che la distribuzione di probabilità del rumore sia gaussiana o meno, ognuno di questi filtri si comporta in maniera più o meno ottima.
Il Filtro di Kalman (sezione 2.12.2) è il filtro ottimo nel caso in cui il problema sia lineare e la distribuzione del rumore gaussiana. I filtri di Kalman Estesi e a Punti Sigma, sezioni 2.12.4 e 2.12.5 rispettivamente, sono filtri sub-ottimi per problemi non-lineari e distribuzione del rumore gaussiana (o poco discostanti da essa). Infine i filtri particellari sono una soluzione sub-ottima per i problemi non lineari con distribuzione del rumore non gaussiana.
I filtri grid-based (sezione 2.12.1) e i filtri particellari (sezione 2.12.8) lavorano su una rappresentazione discreta dello stato, mentre i filtri Kalman, Extendend e Sigma-Point lavorano su una rappresentazione continua dello stato.
Kalman, Kalman Esteso e Kalman a Punti Sigma stimano la distribuzione dell'incertezza (dello stato, del processo, dell'osservazione) come una singola gaussiana. Esistono estensioni multimodali come Multi-hypothesis tracking (MHT) che permettono di applicare i filtri di Kalman a distribuzioni come miscela di gaussiane, mentre i filtri particellari e grid-based sono per loro natura multimodali.
Un ottimo survey sui filtraggi bayesiani è (Che03).