Next: Stima dei Parametri Up: Filtri Bayesiani Previous: Filtro di Kalman a
Gli approcci lineari e quasi lineari proposti da Kalman possono essere usati in quei problemi dove lo stato è gaussiano o quasi gaussiano con distribuzione unimodale: la stima dello stato all'istante di tempo ![]() è funzione diretta dell'unica stima dello stato all'istante di tempo
è funzione diretta dell'unica stima dello stato all'istante di tempo ![]() e della covarianza di tale stima.
e della covarianza di tale stima.
Quando è richiesto di ricavare la distribuzione di probabilità non gaussiana dello stato del sistema
![]() all'istante di tempo
all'istante di tempo ![]() , funzione degli ingressi e delle osservazioni, gli approcci di tipo Kalman non sono più soddisfacenti.
, funzione degli ingressi e delle osservazioni, gli approcci di tipo Kalman non sono più soddisfacenti.
Gli approcci grid based sono adatti a quei problemi, di fatto poco comuni, dove lo stato è discretizzabile e finito. Gli approcci histogram based/occupacy grid si adattano a una classe di problemi maggiore che però, a causa del campionamento uniforme dello stato, scalano molto male con l'aumentare delle dimensioni.
Si consideri nuovamente il risultato espresso dall'equazione (2.4): per estrarre una generica statistica ![]() (per esempio media, o varianza) da una distribuzione di probabilità
(per esempio media, o varianza) da una distribuzione di probabilità ![]() , si fa uso dell'espressione
, si fa uso dell'espressione
Dati i campioni ![]() generati in questo modo, la stima Monte Carlo di
generati in questo modo, la stima Monte Carlo di ![]() è data da
è data da
Monte Carlo non risolve tutti i problemi né suggerisce come ottenere i campioni casuali in maniera efficiente.
Il problema diventa sensibile nei casi multidimensionali dove le aree in cui la probabilità assume valori significativi sono estremamente esigue. L'obiettivo che si pone infatti l'Important Sampling (IS) è campionare la distribuzione ![]() in regioni “importanti” in modo da massimizzare l'efficienza computazionale.
in regioni “importanti” in modo da massimizzare l'efficienza computazionale.
L'idea dell'Important Sampling è quella di prendere una più semplice distribuzione ![]() (Importance density), al posto della vera
(Importance density), al posto della vera ![]() normalmente difficile da campionare (o da riprodurre), effettuando la sostituzione
normalmente difficile da campionare (o da riprodurre), effettuando la sostituzione
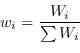 |
(2.131) |
Più la distribuzione ![]() è simile alla
è simile alla ![]() , più la stima risulterà corretta.
D'altra parte la distribuzione
, più la stima risulterà corretta.
D'altra parte la distribuzione ![]() deve essere molto semplice da campionare, scegliendo per esempio la distribuzione uniforme o gaussiana.
deve essere molto semplice da campionare, scegliendo per esempio la distribuzione uniforme o gaussiana.
Data la conoscenza dei filtri bayesiani e con le tecniche Monte Carlo è possibile affrontare la teoria dei filtri particellari.
Lo stato all'istante ![]() è rappresentato da un insieme di campioni (particles) e ogni campione è un ipotesi dello stato da vagliare.
Si può parlare di una serie di particelle ottenute a priori dell'osservazione, applicando l'equazione (2.130) alla funzione di evoluzione dello stato.
è rappresentato da un insieme di campioni (particles) e ogni campione è un ipotesi dello stato da vagliare.
Si può parlare di una serie di particelle ottenute a priori dell'osservazione, applicando l'equazione (2.130) alla funzione di evoluzione dello stato.
Se si applica direttamente la teoria bayesiana ai campioni della distribuzione stimata è possibile modificare i pesi ![]() associati ai campioni usando contemporaneamente il modello del sistema e della percezione (Sequential Important Sampling):
associati ai campioni usando contemporaneamente il modello del sistema e della percezione (Sequential Important Sampling):
Quando possibile è conveniente usare come Important density la distribuzione a priori
| (2.133) |
Il problema dell'approccio SIS è che dopo poche iterazioni solo alcune particelle avranno il fattore peso non trascurabile (weight degeneracy).
Una soluzione più semplice è la Sequential Important Resampling dove i pesi non dipendono dalle iterazioni precedenti ma sono invece i campioni a cambiare, in seguito a una fase di resampling.
La fase di ricampionamento consiste nel generare un nuovo insieme di particelle ![]() ricampionando
ricampionando ![]() volte una versione discreta approssimata di
volte una versione discreta approssimata di
![]() data da
data da
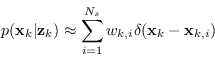 |
(2.135) |
| (2.136) |
I filtri SIR non evitano il caso degenere (di fatto anzi eliminano definitivamente le particelle poco probabili), tuttavia portano a un notevole risparmio computazionale e concentrano la ricerca della soluzione intorno agli stati più probabili.
Esistono svariati algoritmi per eseguire il ricampionamento. Un'elenco, non sicuramente esaustivo, di tali algoritmi è: Simple Random Resampling, Roulette Wheel / Fitness proportionate selection, Stochastic universal sampling, Multinomial Resamping, Residual Resampling, Stratified Resampling, Systematic Resampling.
Paolo medici