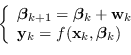Stima dei Parametri
Kalman, in tutte le sue varianti, è classicamente visto come filtro o stimatore di uno stato.
Tuttavia è largamente diffuso, principalmente in machine learning, l'utilizzo di queste tecniche per stimare i parametri di un modello (il meta-modello):
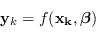 |
(2.137) |
dove 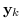 sono le uscite del sistema,
sono le uscite del sistema, 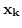 gli ingressi e
gli ingressi e 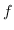 una funzione basata sui parametri
una funzione basata sui parametri
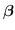 da stimare.
Il concetto di addestramento, o fitting, del modello consiste nel determinare i parametri
da stimare.
Il concetto di addestramento, o fitting, del modello consiste nel determinare i parametri
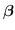 .
.
Kalman permette di determinare i parametri, eventualmente variabili, del modello usando come stato da determinare proprio
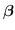 in modo da ottenere un sistema iterativo del tipo
in modo da ottenere un sistema iterativo del tipo
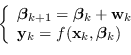 |
(2.138) |
dove il rumore opzionale 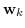 viene usato per modellare eventuali variazioni del modello nel tempo:
la scelta della varianza di
viene usato per modellare eventuali variazioni del modello nel tempo:
la scelta della varianza di 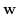 determina la reattività alle variazioni dei parametri del modello.
determina la reattività alle variazioni dei parametri del modello.
Paolo medici
2025-03-12
![]() in modo da ottenere un sistema iterativo del tipo
in modo da ottenere un sistema iterativo del tipo