Filtro alfa beta

L'alpha-beta filter si può vedere come una versione semplificata del filtro di Kalman dove lo stato è rappresentato da sole due variabili di cui una è l'integrale dell'altra. Da una semplice similitudine con sistemi fisici possiamo chiamare queste variabili posizione $\mathbf {x}$ e velocità $\mathbf{v}$. Se si suppone che la velocità rimanga costante nell'intervallo di tempo piccolo $\Delta T$ si ha la stima a priori (predizione) della posizione all'istante $k$ come

$$\hat{\mathbf{x}}^{-}_k = \hat{\mathbf{x}}_{k-1} + \Delta T \mathbf{v}_{k-1}$$ (2.139)

mentre la velocità viene sempre ritenuta costante:

$$\hat{\mathbf{v}}^{-}_k = \hat{\mathbf{v}_{k-1}}$$ (2.140)

L'uscita tuttavia è affetta da rumore e il valore osservato $\mathbf{x}_k$ è differente dal valore predetto $\hat{\mathbf{x}}^{-}_k$. Questo errore di predizione $\mathbf{r}$ è chiamato residuo (stima dell'errore a posteriori):

$$\mathbf{r}_k = \mathbf{x}_k - \hat{\mathbf{x}}^{-}_k$$ (2.141)

Definiamo due parametri $\alpha$ e $\beta$ in modo da ottenere la stima a posteriori come

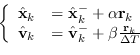$$\left\{ \begin{array}{rl} \hat{\mathbf{x}}_k & = \hat{\math... ...-}_k + \beta \frac{\mathbf{r}_k}{\Delta T} \end{array}\right.$$ (2.142)

In questo modo si ottiene un osservatore asintotico delle variabili posizione e velocità. A differenza del filtro di Kalman, il filtro alfa-beta è un filtro subottimo dove i parametri $\alpha$ e $\beta$ sono tarati per via sperimentale senza nessun riscontro statistico. Questo approccio è solitamente avvallato dal fatto che anche nel filtro di Kalman a volte è necessario imporre le matrici del rumore per via totalmente empirica.