Next: La distribuzione Gaussiana Up: Elementi di Statistica Previous: Elementi di Statistica
È facile supporre che la nozione della media tra numeri sia un concetto conosciuto a tutti, almeno da un punto di vista puramente intuitivo. In questa sezione ne viene comunque fatto un breve riassunto, ne vengono date le definizioni e verranno sottolineati alcuni aspetti interessanti.
Per ![]() campioni di una quantità osservata
campioni di una quantità osservata ![]() la media campionaria sample mean si indica
la media campionaria sample mean si indica ![]() e vale
e vale
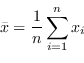 |
(2.1) |
Se si potessero campionare infiniti valori di ![]() ,
, ![]() convergerebbe al valore teorico, atteso (expected value). Questa è la legge dei grandi numeri (Law of Large Numbers).
convergerebbe al valore teorico, atteso (expected value). Questa è la legge dei grandi numeri (Law of Large Numbers).
Il valor medio atteso (expectation, mean) di una variabile casuale ![]() si indica con
si indica con ![]() o
o ![]() e si può calcolare da variabili aleatorie discrete attraverso la formula
e si può calcolare da variabili aleatorie discrete attraverso la formula
![\begin{displaymath}
\E[X] = \mu_x = \sum_{-\infty}^{+\infty} x_i p_X(x_i)
\end{displaymath}](img409.png) |
(2.2) |
![\begin{displaymath}
\E[X] = \mu_x = \int_{-\infty}^{+\infty} x p_X(x) dx
\end{displaymath}](img410.png) |
(2.3) |
Introduciamo ora il concetto di media di una funzione di variabile aleatoria.
Esistono alcune funzioni la cui media assume un significato notevole.
Quando ![]() si parla di statistiche di primo ordine (first statistical moment), e in generale quando
si parla di statistiche di primo ordine (first statistical moment), e in generale quando ![]() si parla di statistiche di
si parla di statistiche di ![]() -ordine.
Il valor medio è pertanto la statistica di primo ordine e un'altra statistica di particolare interesse è il momento di secondo ordine:
-ordine.
Il valor medio è pertanto la statistica di primo ordine e un'altra statistica di particolare interesse è il momento di secondo ordine:
![\begin{displaymath}
\E[X^{2}] = \int_{-\infty}^{+\infty} x^{2} p_X(x) dx
\end{displaymath}](img418.png) |
(2.5) |
La varianza è definita come il valore atteso del quadrato della variabile aleatoria ![]() a cui viene tolto il suo valor medio, ovvero momento di secondo ordine della funzione
a cui viene tolto il suo valor medio, ovvero momento di secondo ordine della funzione ![]() :
:
| (2.6) |
| (2.7) |
La radice quadrata della varianza è conosciuta come deviazione standard (standard deviation) e ha il vantaggio di avere la stessa unità di misura della grandezza osservata:
| (2.8) |
Estendiamo i concetti visti finora al caso multivariabile. Il caso multivariabile può essere visto come estensione a più dimensioni dove ad ogni dimensione è associata una diversa variabile.
La matrice delle covarianze ![]() è l'estensione a più dimensioni (o a più variabili) del concetto di varianza.
È costruita come
è l'estensione a più dimensioni (o a più variabili) del concetto di varianza.
È costruita come
| (2.9) |
I possibili modi di indicare la matrice di covarianza sono
| (2.10) |
La notazione della cross-covarianza è invece univoca
| (2.11) |
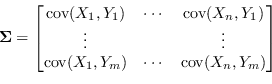 |
(2.12) |
La matrice di covarianza, descrivendo come le variabili sono tra di loro in relazione e di conseguenza quanto sono tra loro slegate, è anche chiamata matrice di dispersione (scatter plot matrix). L'inversa della matrice di covarianza si chiama matrice di concentrazione o matrice di precisione.
La matrice di correlazione
![]() è la matrice di cross-covarianza normalizzata rispetto alle matrici di covarianza:
è la matrice di cross-covarianza normalizzata rispetto alle matrici di covarianza:
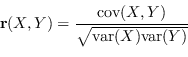 |
(2.13) |
Paolo medici