Next: Filtri Bayesiani Up: Elementi di Statistica Previous: ZCA
In questa sezione sono riportati alcune relazioni di probabilità utili poi nella sezione successiva.
Definiamo la funzione di densità di probabilità (probability density function, PDF) come
| (2.80) |
Il teorema di Bayes (o formula di Bayes) è una relazione che si ottiene unendo il teorema della probabilità composta con il teorema della probabilità assoluta.
Partendo dalla definizione di probabilità condizionata
![]() (multiplication rule) si ottiene:
(multiplication rule) si ottiene:
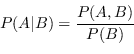 |
(2.81) |
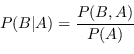 |
(2.82) |
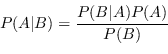 |
(2.83) |
Si può applicare lo stesso ragionamento nel caso di tre variabili:
| (2.84) |
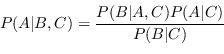 |
(2.85) |
Un'altra formula importante che verrà usata nella prossima sezione è il teorema della probabilità assoluta (law of total probability):
| (2.86) |
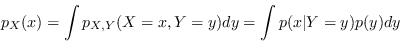 |
(2.87) |
Paolo medici