Rumore correlato

Nel caso in cui il rumore non sia semplicemente additivo, ma si propaghi nel sistema attraverso una trasformazione comunque lineare, il sistema di Kalman si generalizza in

$$\left\{ \begin{array}{l} \mathbf{x}_{k+1} = \mathbf{A}_{k} ... ... \mathbf{x}_{k} + \mathbf{V}_k \mathbf{v}_k \end{array}\right.$$ (2.115)

Il rumore di processo è correlato attraverso una matrice $\mathbf{W}_k$ alla sorgente, e il rumore di osservazione attraverso una matrice $\mathbf{V}_k$.

È possibile in questo caso applicare le stesse equazioni del sistema di Kalman introducendo le sostituzioni

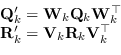$$\begin{array}{l} \mathbf{Q}'_k = \mathbf{W}_k \mathbf{Q}_k \... ..._k = \mathbf{V}_k \mathbf{R}_k \mathbf{V}^{\top}_k \end{array}$$ (2.116)

Tale risultato tornerà utile nella sezione seguente sul filtro di Kalman esteso.

Chiaramente se le matrici $\mathbf{W}_k$ e $\mathbf{V}_k$ sono delle identità, ovvero il rumore è semplicemente additivo, la forma si semplifica e ridiventa quella vista in precedenza.