Next: Rumore correlato Up: Filtri Bayesiani Previous: Metodi Grid-based
Il filtro di Kalman (WB95) cerca di stimare in presenza di disturbi lo stato interno
![]() , non accessibile, di un sistema tempo discreto, la cui conoscenza del modello è completa.
Di fatto il filtro di Kalman è lo stimatore ricorsivo ottimo: se il rumore del problema è gaussiano, il filtro di Kalman fornisce la stima ai minimi quadrati dello stato interno del sistema.
, non accessibile, di un sistema tempo discreto, la cui conoscenza del modello è completa.
Di fatto il filtro di Kalman è lo stimatore ricorsivo ottimo: se il rumore del problema è gaussiano, il filtro di Kalman fornisce la stima ai minimi quadrati dello stato interno del sistema.
Per ragioni storiche il filtro di Kalman si riferisce propriamente al solo filtraggio di un sistema dove la transizione di stato e l'osservazione sono funzioni lineari dello stato corrente.
Seguendo la teoria dei sistemi lineari, la dinamica di un sistema “lineare” tempo continuo è rappresentata da una equazione differenziale del tipo
| (2.98) |
| (2.99) |
Il filtro di Kalman a tempo discreto viene in aiuto dei sistemi reali dove il mondo viene campionato a intervalli discreti, trasformando il sistema lineare tempo continuo in un sistema lineare del tipo
Le variabili ![]() e
e ![]() rappresentano rispettivamente il rumore di processo e di osservazione, valor medio nullo
rappresentano rispettivamente il rumore di processo e di osservazione, valor medio nullo
![]() e varianza rispettiva
e varianza rispettiva ![]() e
e ![]() conosciute (si suppone rumore gaussiano bianco).
conosciute (si suppone rumore gaussiano bianco). ![]() è una matrice
è una matrice ![]() di transizione dello stato,
di transizione dello stato, ![]() è una matrice
è una matrice ![]() che collega l'ingresso di controllo opzionale
che collega l'ingresso di controllo opzionale
![]() con lo stato
con lo stato ![]() e infine
e infine ![]() è una matrice
è una matrice ![]() che collega lo stato con la misura
che collega lo stato con la misura
![]() .
Tutte queste matrici, rappresentanti il modello del sistema, devono essere conosciute con assoluta precisione, pena l'introduzione di errori sistematici.
.
Tutte queste matrici, rappresentanti il modello del sistema, devono essere conosciute con assoluta precisione, pena l'introduzione di errori sistematici.
Il filtro di Kalman è un filtro di stima ricorsivo e richiede ad ogni iterazione la conoscenza dello stato stimato dal passo precedente
![]() e l'osservazione corrente
e l'osservazione corrente ![]() , osservazione indiretta dello stato del sistema.
, osservazione indiretta dello stato del sistema.
Sia
![]() la stima a priori dello stato del sistema, basata sulla stima ottenuta al tempo
la stima a priori dello stato del sistema, basata sulla stima ottenuta al tempo ![]() e dalla dinamica del problema, e
e dalla dinamica del problema, e
![]() la stima dello stato del problema a posteriori dell'osservazione
la stima dello stato del problema a posteriori dell'osservazione ![]() e basata su di essa.
Da queste definizioni è possibile definire l'errore della stima a priori e a a posteriori come
e basata su di essa.
Da queste definizioni è possibile definire l'errore della stima a priori e a a posteriori come
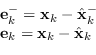 |
(2.101) |
![\begin{displaymath}
\begin{array}{l}
\mathbf{P}^{-}_k = \E[\mathbf{e}^{-}_k {\m...
...\mathbf{P}_k = \E[\mathbf{e}_k \mathbf{e}^{\top}_k]
\end{array}\end{displaymath}](img694.png) |
(2.102) |
L'obiettivo del filtro di Kalman è minimizzare la covarianza dell'errore a posteriori ![]() e fornire un metodo per ottenere la stima di
e fornire un metodo per ottenere la stima di
![]() data la stima a priori
data la stima a priori
![]() e l'osservazione
e l'osservazione ![]() .
.
Il filtro di Kalman fornisce una stima dello stato a posteriori attraverso una combinazione lineare della stima dello stato precedente e dell'errore di osservazione:
Il filtro di Kalman viene normalmente presentato in due fasi: aggiornamento del tempo (fase di predizione) e aggiornamento della misura (fase di osservazione).
Nella prima fase si ottiene la stima a priori sia di
![]() che della covarianza
che della covarianza
![]() .
La stima a priori
.
La stima a priori
![]() viene dalla buona conoscenza della dinamica del sistema (2.100):
viene dalla buona conoscenza della dinamica del sistema (2.100):
| (2.105) |
Queste sono le miglior stime dello stato e della covarianza dell'istante ![]() ottenibili a priori dell'osservazione del sistema.
ottenibili a priori dell'osservazione del sistema.
Nella seconda fase viene calcolato il guadagno
Usando questo valore per il guadagno ![]() , la stima a posteriori della matrice di covarianza diventa
, la stima a posteriori della matrice di covarianza diventa
Per poter unificare le diverse varianti dei filtri di Kalman si possono tradurre queste equazioni usando le matrici di varianza-covarianza
Come si può facilmente notare la matrice di covarianza e il guadagno di Kalman non dipendono minimamente né dallo stato, ne dalle osservazioni, ne tanto meno dal residuo, e hanno una storia indipendente.
Kalman richiede tuttavia un valore iniziale della variabile di stato e della matrice di covarianza: il valore iniziale dello stato deve essere il più simile possibile al valore vero e la somiglianza a questo valore va inserita nella matrice di covarianza iniziale.
È interessante mostrare, come esempio, il caso semplificato di filtro di Kalman di stato monodimensionale e coincidente con l'osservabile.
Le equazioni di transizione e di osservazioni sono
 |
(2.111) |
Il ciclo di predizione è molto semplice e diventa:
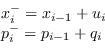 |
(2.112) |
Il guadagno di Kalman ![]() diventa
diventa
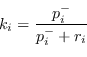 |
(2.113) |
È solitamente possibile stimare a priori il valore di ![]() , mentre quello di
, mentre quello di ![]() va impostato attraverso esperimenti.
va impostato attraverso esperimenti.
Come si vede nella prima delle equazioni (2.114), il fattore ![]() è di fatto un blending factor tra l'osservazione dello stato e lo stato stimato precedente.
è di fatto un blending factor tra l'osservazione dello stato e lo stato stimato precedente.
Nel caso monodimensionale è facile vedere come il guadagno ![]() e la varianza
e la varianza ![]() sono processi indipendenti dallo stato e dalle osservazioni, tanto meno dall'errore.
Se
sono processi indipendenti dallo stato e dalle osservazioni, tanto meno dall'errore.
Se ![]() e
e ![]() non variano nel tempo,
non variano nel tempo, ![]() e
e ![]() sono sequenze numeriche che convergono a un numero costante determinato solamente dalla caratterizzazione del rumore, indipendentemente dai valori assunti all'inizio. Si confronti questo risultato con quello che si ottiene dall'equazione (2.70).
sono sequenze numeriche che convergono a un numero costante determinato solamente dalla caratterizzazione del rumore, indipendentemente dai valori assunti all'inizio. Si confronti questo risultato con quello che si ottiene dall'equazione (2.70).
Paolo medici