Media ponderata con la varianza

Avendo molteplici osservazioni con varianza differente $\sigma^{2}_i$, si vogliono fondere le varie osservazioni. Questo è il caso per esempio di più osservazioni dello stesso osservabile eseguite da diversi sensori nello stesso istante o con lo stesso sensore di una quantità supposta costante ma con rumore di osservazione variabile nel tempo. L'obiettivo è ottenere una media pesata di ogni singola osservazione del tipo

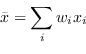$$\bar{x} = \sum_i w_i x_i$$ (2.65)

La varianza della variabile $\bar{x}$ sarà per definizione.

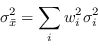$$\sigma^2_{\bar{x}} = \sum_i w^{2}_i \sigma^2_{i}$$ (2.66)

La soluzione ottima (stimatore di massima verosimiglianza) si ottiene minimizzando questa quantitá sotto il vincolo aggiuntivo $\sum_i w_i = 1$.

Il peso che minimizza questa quantità è

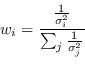$$w_i = \frac{ \frac{1}{\sigma^{2}_i} } { \sum_j \frac{1}{\sigma^{2}_j} }$$ (2.67)

In questo modo la varianza della media è inferiore alla varianza dei singoli strumenti di misura ed equivale a

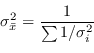$$\sigma^{2}_{\bar{x}} = \frac{1}{\sum 1/\sigma^{2}_i}$$ (2.68)

Conseguenza diretta è il poter unire $n$ letture dello stesso sensore e dello stesso osservabile (supponendo il rumore di osservazione a varianza costante) ma in istanti di tempo differenti. La varianza finale si riduce a

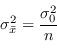$$\sigma^{2}_{\bar{x}} = \frac{ \sigma^{2}_0 } {n}$$ (2.69)

È possibile costruire in modo iterativo questo risultato attraverso la successione:

$$\bar{x}_{i+1} = (1 - k) \bar{x}_i + k x_{i+1} \quad k = \frac{\sigma^2_{\bar{x} } } { \sigma^2_{\bar{x} } + \sigma^2_{i+1} }$$ (2.70)

con $k$ fattore di blending. Scritta in questo modo, la stima dell'osservabile è nella stessa forma del filtro di Kalman monodimensionale (si confronti questo risultato con quello di sezione 2.12.2): senza rumore di processo, il guadagno $k$ è tendente a zero.