Stima del Massimo a Posteriori

Il Maximum a Posteriori estimator, o maximum a posteriori probability (MAP), fornisce come stima (una delle) moda della distribuzione a posteriori. A differenza della stima alla massima verosimiglianza, la MAP ottiene una densità a posteriori facendo uso della teoria bayesiana, unendo la conoscenza a priori 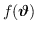$f(\boldsymbol\vartheta)$ con la densità condizionale 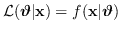$\mathcal{L}(\boldsymbol\vartheta \vert \mathbf{x}) = f(\mathbf{x} \vert \boldsymbol\vartheta)$ di verosimiglianza, ottenendo la nuova stima

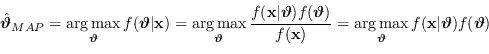$$\hat{\boldsymbol\vartheta}_{MAP} = \argmax_{\boldsymbol\vart... ...mathbf{x} \vert \boldsymbol\vartheta) f(\boldsymbol\vartheta)$$ (2.63)

e nel caso di eventi non correlati la formula si trasforma in

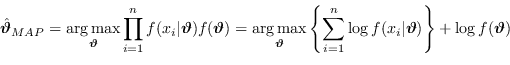$$\hat{\boldsymbol\vartheta}_{MAP} = \argmax_{\boldsymbol\vart... ...\boldsymbol\vartheta) \right\} + \log f(\boldsymbol\vartheta)$$ (2.64)

dove, sempre per semplificare i conti, si sono sfruttate le proprietà del logaritmo.

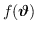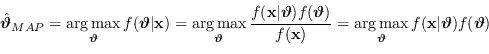
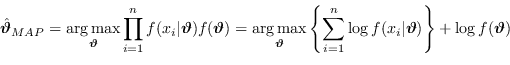
Chiaramente se la probabilità a priori $f(\boldsymbol\vartheta)$ è uniforme, MAP e MLE sono coincidenti.