Next: Stima del Massimo a Up: Elementi di Statistica Previous: Condizionamento nei sistemi lineari
Da un punto di vista statistico il vettore dei dati
![]() sono realizzazioni di una variabile aleatoria di una popolazione sconosciuta.
Il compito dell'analisi dei dati è quella di individuare la popolazione che più probabilmente ha generato quei campioni. In statistica, ogni popolazione è identificata da una corrispondente distribuzione
di probabilità e associata a ogni distribuzione di probabilità c'è una parametrizzazione unica
sono realizzazioni di una variabile aleatoria di una popolazione sconosciuta.
Il compito dell'analisi dei dati è quella di individuare la popolazione che più probabilmente ha generato quei campioni. In statistica, ogni popolazione è identificata da una corrispondente distribuzione
di probabilità e associata a ogni distribuzione di probabilità c'è una parametrizzazione unica
![]() : variando questi parametri deve essere generata una differente distribuzione di probabilità.
: variando questi parametri deve essere generata una differente distribuzione di probabilità.
Sia
![]() la funzione di densità di probabilità (PDF) che indica la probabilità di osservare
la funzione di densità di probabilità (PDF) che indica la probabilità di osservare ![]() data una parametrizzazione
data una parametrizzazione
![]() .
Se le osservazioni singole
.
Se le osservazioni singole ![]() sono statisticamente indipendenti una dall'altra la PDF di
sono statisticamente indipendenti una dall'altra la PDF di ![]() può essere espressa come prodotto delle singole PDF:
può essere espressa come prodotto delle singole PDF:
| (2.53) |
Data una parametrizzazione
![]() è possibile definire una specifica PDF che mostra la probabilità di comparire di alcuni dati rispetto ad altri.
Nel caso reale abbiamo esattamente il problema reciproco: i dati sono stati osservati e c'è da individuare quale
è possibile definire una specifica PDF che mostra la probabilità di comparire di alcuni dati rispetto ad altri.
Nel caso reale abbiamo esattamente il problema reciproco: i dati sono stati osservati e c'è da individuare quale
![]() ha generato quella specifica PDF.
ha generato quella specifica PDF.
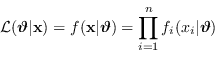 |
(2.54) |
Il principio dello stimatore a massima verosimiglianza (MLE)
![]() , sviluppato originariamente da R.A. Fisher negli anni '20 del novecento, sceglie come migliore parametrizzazione quella che fa adattare meglio la distribuzione di probabilità generata con i dati osservati.
, sviluppato originariamente da R.A. Fisher negli anni '20 del novecento, sceglie come migliore parametrizzazione quella che fa adattare meglio la distribuzione di probabilità generata con i dati osservati.
Nel caso di distribuzione di probabilità gaussiana è utile una ulteriore definizione.
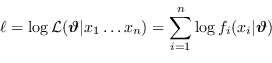 |
(2.55) |
La miglior stima dei parametri del modello è quella che massimizza la verosimiglianza, ovvero la verosimiglianza logaritmica
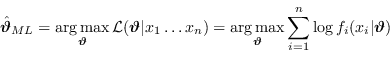 |
(2.56) |
È possibile trovare in letteratura, come stimatore ottimo, invece del massimo della funzione di verosimiglianza, il minimo dell'opposta
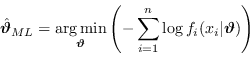 |
(2.57) |
Questa formulazione risulta molto utile quando la distribuzione del rumore è gaussiana.
Siano ![]() le realizzazioni della variabile aleatoria.
Nel caso infatti di una generica funzione
le realizzazioni della variabile aleatoria.
Nel caso infatti di una generica funzione
![]() con rumore a distribuzione normale, tempo costante e media nulla, la Likelihood è
con rumore a distribuzione normale, tempo costante e media nulla, la Likelihood è
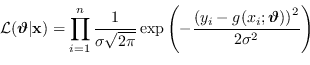 |
(2.58) |
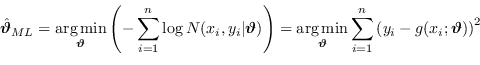 |
(2.59) |
Ora, le ![]() derivate parziali della log-verosimiglianza formano un vettore
derivate parziali della log-verosimiglianza formano un vettore ![]()
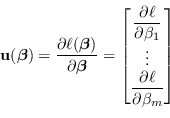 |
(2.60) |
| (2.61) |
![\begin{displaymath}
\var \left( \mathbf{u}(\boldsymbol\beta) \right) = \E \left[...
...ta_j \partial \beta_k} \right] = \mathcal{I}(\boldsymbol\beta)
\end{displaymath}](img586.png) |
(2.62) |