Metodi Grid-based

Gli approcci grid-based si adattano perfettamente a quei problemi dove lo stato assume solo un numero limitato di valori discreti (vengono infatti detti Filtri Discreti) mentre permettono di fornire una stima approssimata nel caso di stato continuo (histogram filters) trasformato in discreto attraverso una quantizzazione spaziale. Ad ogni elemento della griglia (o dell'istogramma) è associata la probabilità che lo stato sia effettivamente in quella particolare cella. La teoria dei filtri bayesiani (perciò distribuzioni multimodali e sistemi fortemente non lineari) è sfruttata direttamente, limitata però ai soli punti discreti in cui lo stato può vivere.

Si supponga che vengano usati $m$ punti per rappresentare lo stato $\mathbf{x} \in \mathbb{R}^{n}$. Se lo stato originale è continuo questa è chiaramente una approssimazione ed è preferibile che $m \gg n$. Ad ogni iterazione $k$, esistono pertanto $\mathbf{x}_{i,k} \in \mathbb{R}^{n}$ con $i=1,\ldots,m$ stati possibili a cui è associata una distribuzione di probabilità $p_{i,k}$ che si evolve nel tempo in base alla dinamica del problema.

Valgono le equazioni viste in precedenza, ovvero la stima a priori:

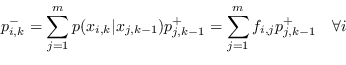$$p^{-}_{i,k} = \sum_{j=1}^{m} p(x_{i,k} \vert x_{j,k-1}) p^{+}_{j,k-1}= \sum_{j=1}^{m} f_{i,j} p^{+}_{j,k-1} \quad \forall i$$ (2.96)

e l'equazione di aggiornamento dello stato a posteriori dell'osservazione $z_k$:

$$p^{+}_{i,k} = c_k p(z_k \vert x_{i,k}) p^{-}_{i,k} \quad \forall i$$ (2.97)

con $c_k$ sempre fattore di normalizzazione tale che $\sum p^{+}_i = 1$.

I metodi grid-based permettono di applicare pertanto la teoria ricorsiva bayesiana direttamente.