Next: Condizionamento nei sistemi lineari Up: Propagazione dell'incertezza Previous: Esempi di propagazione degli
Per stimare valor medio e varianza, la variabile casuale in ingresso
![]() viene approssimata da
viene approssimata da ![]() punti
punti
![]() , chiamati sigma points, ognuno pesato con un peso
, chiamati sigma points, ognuno pesato con un peso ![]() , in modo da ottenere una distribuzione con media e varianza
, in modo da ottenere una distribuzione con media e varianza
![]() e
e
![]() rispettivamente, ovvero parametri esattamente uguali a quelli di
rispettivamente, ovvero parametri esattamente uguali a quelli di ![]() .
.
Un modo per ottenere un insieme di punti, la cui distribuzione ha media e varianza uguali a quelli della distribuzione originale, consiste nel prendere ![]() sigma-points e i rispettivi pesi nel modo seguente:
sigma-points e i rispettivi pesi nel modo seguente:
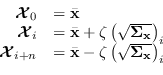 |
(2.42) |
A differenza dei metodi montecarlo, i sigma-points sono scelti in maniera deterministica in modo da rappresentare al meglio le statistiche della variabile.
Ottenuti i sigma-points, questi vengono trasformati (unscented transformation) attraverso la funzione ![]() in punti sigma trasformati
in punti sigma trasformati
| (2.43) |
Da questi punti è possibile calcolare media e varianza della variabile di uscita attraverso
Il problema affrontato dall'approccio a punti Sigma è comunque un problema mal definito perché esistono infinite distribuzioni di probabilità possedenti la stessa la media e la covarianza.
La Unscented transform (UT) (JU97), una dei possibili Sigma-Point Approach, fissa come valori
![]() ,
dove
,
dove ![]() è la dimensione dello spazio e
è la dimensione dello spazio e ![]() è un numero definito come
è un numero definito come
![]() con
con
![]() un numero piccolo positivo e
un numero piccolo positivo e ![]() solitamente posto a
solitamente posto a ![]() o
o ![]() .
In alcuni articoli viene posto
.
In alcuni articoli viene posto ![]() e
e ![]() per le distribuzioni gaussiane.
per le distribuzioni gaussiane.
Anche nella trasformazione unscented i punti sigma sono punti pesati e i pesi sono differenti nel calcolo del valor medio e della matrice di covarianza.
La trasformazione unscented fissa pertanto questi pesi a
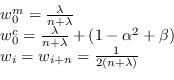 |
(2.45) |
È da sottolineare che le varianti degli approcci sigma-point hanno tali pesi calcolati in maniera differente.
Paolo medici