Next: Propagazione dell'errore attraverso statistiche Up: Propagazione dell'incertezza Previous: Propagazione dell'incertezza
Risulta importante nel campo della visione artificiale la teoria della propagazione degli errori, in quanto sono comuni operazioni base di estrazione di caratteristiche affette da rumore, come per esempio la misura dell'intensità di colore o la misura della posizione di una particolare feature sull'immagine, ed è importante capire quanto questo rumore influisce nei calcoli successivi.
L'errore di misura dovuto a rumore additivo si formalizza come
![]() , dove
, dove ![]() è il valore osservato,
è il valore osservato, ![]() il valore reale e
il valore reale e ![]() è il rumore additivo, per esempio gaussiano bianco di varianza
è il rumore additivo, per esempio gaussiano bianco di varianza
![]() .
.
Nel caso della visione potrebbe essere interessante stimare come si propaga nel sistema l'errore generato dall'osservazione imprecisa di un punto sull'immagine.
In questo caso le variabili osservate saranno ![]() coordinate immagine affette entrambe da errore di localizzazione di varianza
coordinate immagine affette entrambe da errore di localizzazione di varianza
![]() e
e
![]() rispettivamente,
variabili normalmente (almeno in prima approssimazione) non correlate tra di loro.
rispettivamente,
variabili normalmente (almeno in prima approssimazione) non correlate tra di loro.
Usando il risultato di equazione (2.33), la generica funzione ![]() , funzione in due variabili aleatorie, si può approssimare al primo ordine attraverso l'espansione in serie di Taylor come
, funzione in due variabili aleatorie, si può approssimare al primo ordine attraverso l'espansione in serie di Taylor come
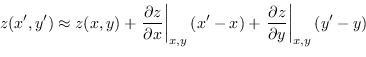 |
(2.35) |
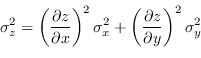 |
(2.36) |
Con questa formulazione, si possono presentare alcuni esempi:
| (2.37) |
| (2.38) |
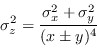 |
(2.39) |
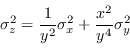 |
(2.40) |
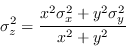 |
(2.41) |
È interessante notare da queste equazioni come il valore assoluto che assumono le variabili (![]() e
e ![]() negli esempi) influisca direttamente sulla stima dell'errore sulla variabile finale
negli esempi) influisca direttamente sulla stima dell'errore sulla variabile finale ![]() : alcune variabili producono risultati a varianza inferiore man mano che aumentano di intensità, mentre altre possono avere un comportamento contrario.
Per questi motivi, a seconda della trasformazione e pertanto della stima del modello che si vuole ottenere, alcuni punti dell'immagine possono essere più importanti da osservare rispetto ad altri.
: alcune variabili producono risultati a varianza inferiore man mano che aumentano di intensità, mentre altre possono avere un comportamento contrario.
Per questi motivi, a seconda della trasformazione e pertanto della stima del modello che si vuole ottenere, alcuni punti dell'immagine possono essere più importanti da osservare rispetto ad altri.
Paolo medici