Next: Parametrizzazioni alternative nello spazio Up: Elementi Previous: Sistemi lineari sovradimensionati
Gli autovalori e autovettori sono stati già anticipati nella sezione precedente. In questa verrà fatta una trattazione minimale per poterli usare in maniera proficua.
Riscrivendo il sistema (1.10) usando la matrice identità ![]() , segue che autovalore e autovettore associato si ottengono come soluzione del sistema omogeneo:
, segue che autovalore e autovettore associato si ottengono come soluzione del sistema omogeneo:
Se ![]() è un autovettore di
è un autovettore di ![]() associato all'autovalore
associato all'autovalore ![]() e
e ![]() un numero (reale o complesso), allora anche
un numero (reale o complesso), allora anche ![]() è un autovettore di
è un autovettore di ![]() .
.
In generale l'insieme dei vettori ![]() associati a un autovalore
associati a un autovalore ![]() di
di ![]() forma un sottospazio di
forma un sottospazio di
![]() chiamato autospazio.
La dimensione di questo sottospazio è detta molteplicità geometrica dell'autovalore.
chiamato autospazio.
La dimensione di questo sottospazio è detta molteplicità geometrica dell'autovalore.
Dalla definizione (1.11) si evince che ![]() è un autovalore se e solo se
è un autovalore se e solo se ![]() .
Le radici del polinomio caratteristico sono gli autovalori di
.
Le radici del polinomio caratteristico sono gli autovalori di ![]() e di conseguenza il polinomio caratteristico ha grado pari alla dimensione della matrice.
Le matrici
e di conseguenza il polinomio caratteristico ha grado pari alla dimensione della matrice.
Le matrici ![]() e
e ![]() hanno polinomi caratteristici notevoli.
hanno polinomi caratteristici notevoli.
| (1.13) |
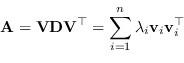 |
(1.14) |