Next: Coordinate Polari Up: Elementi Previous: Autovalori e Autovettori
I punti nei vari spazi ![]() possono essere descritti con coordinate diverse da quelle cartesiane. In questa sezione vengono presentate alcune parametrizzazioni utili che verranno usate nel resto del libro.
possono essere descritti con coordinate diverse da quelle cartesiane. In questa sezione vengono presentate alcune parametrizzazioni utili che verranno usate nel resto del libro.
Introduciamo la seguente definizione:
| (1.15) |
Nel caso ![]() la “sfera” unitaria
la “sfera” unitaria
![]() è formata da solo 2 punti e perciò non è una varietà connessa.
è formata da solo 2 punti e perciò non è una varietà connessa.
Con ![]() la varietà è esattamente la stessa di
la varietà è esattamente la stessa di ![]() ovvero con la parametrizzazione
ovvero con la parametrizzazione
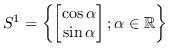 .
.
La sfera ![]() (la superficie della sfera o una direzione in
(la superficie della sfera o una direzione in ![]() ) invece è una 2-varietà che non ha struttura di gruppo. Può essere parametrizzata da due parametri (ad esempio le coordinate polari come vedremo tra poco) ma presenterà sempre delle singolarità.
) invece è una 2-varietà che non ha struttura di gruppo. Può essere parametrizzata da due parametri (ad esempio le coordinate polari come vedremo tra poco) ma presenterà sempre delle singolarità.