Coordinate Polari

Dando per assodate le coordinate cartesiane, in questa sezione vengono introdotte le coordinate polari e in particolare verranno mostrate le relazioni che legano le coordinate cartesiane a quelle polari.

Figura 1.1: Corrispondenza tra coordinate polari e cartesiane.

Per un punto nello spazio bidimensionale la relazione che lega questi due sistemi di coordinate si scrive come:

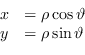$$\begin{array}{rl} x &= \rho \cos \vartheta \\ y &= \rho \sin \vartheta \\ \end{array}$$ (1.16)

La trasformazione inversa, da cartesiane a polari, è

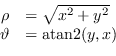$$\begin{array}{rl} \rho &= \sqrt{x^2+y^2} \\ \vartheta &= \operatorname{atan2} (y,x) \\ \end{array}$$ (1.17)

Un punto su una sfera non ha invece una rappresentazione univoca: per lo stesso motivo, come verrà sottolineato più volte in appendice, esistono infinite rappresentazioni di una rotazione nello spazio tridimensionale.

Una scelta molto diffusa sono le coordinate polari sferiche (sperical coordinate system).

Figura 1.2: Coordinate polari in 3 dimensioni: coordinate sferiche.

Con questa convenzione la relazione tra le coordinate cartesiane e quelle polari si scrive

$$\begin{array}{rl} x &= \rho \sin \vartheta \cos \varphi ... ...heta \sin \varphi \\ z &= \rho \cos \vartheta \\ \end{array}$$ (1.18)

dove $\vartheta$ è definito come zenit mentre $\varphi$ è chiamato azimuth.

La trasformazione inversa, da coordinate cartesiane a polari, si ottiene come

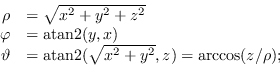$$\begin{array}{rl} \rho &= \sqrt{x^2+y^2+z^2} \\ \varphi&=... ...torname{atan2}(\sqrt{x^2+y^2},z) = \arccos(z/\rho); \end{array}$$ (1.19)