Next: Coordinate Omogenee Up: Parametrizzazioni alternative nello spazio Previous: Coordinate Polari
Una alternativa abbastanza comune per parametrizzare la sfera ![]() è usare la proiezione stereografica per trasformare coordinate dallo spazio della varietà
è usare la proiezione stereografica per trasformare coordinate dallo spazio della varietà
![]() (spazio parametri) a
(spazio parametri) a
![]() (spazio cartesiano) e viceversa.
(spazio cartesiano) e viceversa.
Nella sfera tridimensionale ![]() , è possibile definire una funzione
, è possibile definire una funzione ![]() come proiezione stereografica dallo spazio
come proiezione stereografica dallo spazio
![]() a
a
![]() :
:
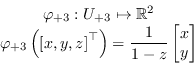 |
(1.20) |
![\begin{displaymath}
\varphi_{+3}^{-1} \left( \left[u,v \right]^{\top} \right) =...
... \begin{bmatrix}
2u \\
2v \\
-1 + u^2 + v^2
\end{bmatrix}\end{displaymath}](img123.png) |
(1.21) |
Allo stesso modo possono essere definiti degli spazi
![]() dove gli
dove gli ![]() sono i versori unitari dentro i quali definire 6 parametrizzazioni simili (ognuna con la sua diversa singolarità) e questo permette di scegliere la parametrizzazione più opportuna in modo da operare nel punto più distante dalla singolarità di quella specifica formula.
sono i versori unitari dentro i quali definire 6 parametrizzazioni simili (ognuna con la sua diversa singolarità) e questo permette di scegliere la parametrizzazione più opportuna in modo da operare nel punto più distante dalla singolarità di quella specifica formula.
Paolo medici