Coordinate Omogenee

In questa sezione vengono introdotte le coordinate omogenee, un artificio matematico che risulta molto utile per la discussione del problema della geometria proiettiva ma anche di diversi formalismi affrontati in diversi capitoli di questo libro.

Chiameremo coordinate omogenee (homogeneous coordinates) di un punto del piano $\mathbf{p} = ( x, y ) \in \mathbb{R}^{2}$ una qualsiasi terna ordinata $\mathbf{\tilde{p}} =(x', y', w') \in \mathbb{R}^{3}$ di numeri reali tali che $w' \neq 0$, $\frac{x'}{w'} = x$ e $\frac{y'}{w'} = y$. Allo stesso modo coordinate omogenee di un punto $\mathbf{p} = ( x, y, z ) \in \mathbb{R}^{3}$ saranno una quadrupla di numeri $\mathbf{\tilde{p}} =(x', y', z', w') \in \mathbb{R}^{4}$ tali che $w' \neq 0$ e $\frac{x'}{w'} = x$, $\frac{y'}{w'} = y$ e $\frac{z'}{w'} = z$.

Il punto $\mathbf{\tilde{p}}$ espresso in coordinate omogenee equivale al punto reale $\mathbf {p}$ (inhomogeneous):

$$\mathbf{\tilde{p}} = ( x',y',w' ) = w' (\frac{x'}{w'},\frac{y'}{w'},1) = w' (x,y,1) = w' \mathbf{p}$$

Il vettore $(x,y,1)$ è chiamato augmented vector.

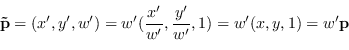
Le coordinate omogenee hanno le seguenti proprietà:

• Le coordinate omogenee sono definite a meno di un coefficiente di proporzionalità. Ad esempio, la terna $(x,y,1)$ ed ogni suo multiplo $\lambda \neq 0$, ovvero $( x, y, 1 ) \cong ( \lambda x, \lambda y, \lambda )$, sono coordinate omogenee dello stesso punto dello spazio $(x,y)$;
• I punti in coordinate omogenee con coordinata $w=0$ sono detti impropri, points at infinity o ideal points, e non hanno nessun significato geometrico nello spazio cartesiano, ma possono rappresentare un punto all'infinito, nella direzione del vettore $(x,y)$.

In coordinate omogenee c'è pertanto distinzione tra vettore ($w=0$) e punto ($w \neq 0$), cosa che non accade con le coordinate euclidee. L'insieme costituito da tutte le terne/quaterne non nulle forma uno spazio proiettivo bidimensionale/tridimensionale.

Le coordinate omogenee permettono di rappresentare punti all'infinito e consentono di esprimere tutte le trasformazioni di coordinate geometriche usate in visione artificiale in forma matriciale. L'uso di coordinate omogenee è usato in computer graphics per la proprietà di rappresentare, esattamente come nel caso cartesiano, le trasformazioni affini attraverso l'uso di matrici ed in più permettono di rappresentare con lo stesso formalismo anche le proiezioni prospettiche.