Next: Total Least Squares Up: Regressione ai minimi quadrati Previous: Regressione ai minimi quadrati
Quando ![]() è una funzione lineare rispetto ai parametri
è una funzione lineare rispetto ai parametri
![]() si parla di regressione lineare ai minimi quadrati (Linear Least Squares o Ordinary Least Squares OLS).
Tale funzione può essere rappresentata nella forma di sistema lineare
si parla di regressione lineare ai minimi quadrati (Linear Least Squares o Ordinary Least Squares OLS).
Tale funzione può essere rappresentata nella forma di sistema lineare
Ogni osservazione è un vincolo e tutti i singoli vincoli possono essere raccolti in forma matriciale
| (3.13) |
L'obiettivo è quello di trovare l'iperpiano
![]() in
in ![]() dimensioni che meglio si adatta ai dati
dimensioni che meglio si adatta ai dati
![]() .
.
Il valore
![]() che minimizza la funzione costo definita in equazione (3.6), limitatamente al caso di rumore sull'osservazione a valor medio nullo e varianza costante fra tutti i campioni, di fatto è il miglior stimatore lineare che minimizza la varianza (Best Linear Unbiased Estimator BLUE).
che minimizza la funzione costo definita in equazione (3.6), limitatamente al caso di rumore sull'osservazione a valor medio nullo e varianza costante fra tutti i campioni, di fatto è il miglior stimatore lineare che minimizza la varianza (Best Linear Unbiased Estimator BLUE).
Il teorema di Gauss-Markov dimostra che uno stimatore ai minimi quadrati è la miglior scelta tra tutti gli stimatori a minima varianza BLUE quando la varianza sull'osservazione è costante (homoscedastic).
La miglior stima ai minimi quadrati
![]() che minimizza la somma dei residui è la soluzione del problema lineare
che minimizza la somma dei residui è la soluzione del problema lineare
| (3.14) |
La matrice ![]() , definita come
, definita come
| (3.15) |
| (3.16) |
Nel caso di rumore a varianza non costante tra i campioni osservati (heteroscedastic) la regressione a minimi quadrati pesata è la scelta BLUE
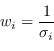 |
(3.17) |
| (3.18) |
Generalizzando ulteriormente, nel caso di rumore con varianza non costante tra i campioni osservati e tra loro correlato, la miglior stima BLUE nel caso lineare deve tenere conto della covarianza del rumore
![]() :
:
| (3.19) |
Tale sistema minimizza la varianza
| (3.20) |
Paolo medici