Trasformata di Hough

Figura: Esempio di Trasformata di Hough per individuare rette in coordinate polari: mappa accumulatore (in alto a destra) di un singolo punto (in alto a sinistra), e mappa accumulatore (in basso a destra) di una serie di punti colineari insieme ad outlier (in basso a sinistra).

Sia $g(\mathbf{x}, \boldsymbol\beta)=0$ una varietà continua in $\mathbf {x}$ di cui è richiesto stimare i parametri $\boldsymbol\beta \in \mathbb{R}^m$. Per ricavare tali parametri e poter definire completamente la funzione, sono disponibili un insieme di coordinate $S = \left\{ \mathbf{x}_1, \ldots, \mathbf{x}_n \right\}$ che appartengono al luogo dei punti della funzione, potenzialmente affetti da rumore ma sopratutto potenzialmente outlier.

La trasformata di Hough (Hough Transform) è una tecnica che permette di raggruppare un insieme “molto probabile” di punti che soddisfano alcuni vincoli parametrici (PIK92).

Per ogni possibile punto $\boldsymbol\beta^{*}$ nello spazio dei parametri è possibile associare un voto $H(\boldsymbol\beta)$ del tipo

$$H(\boldsymbol\beta^{*}) = \left\{ \mathbf{x} : g(\mathbf{x}, \boldsymbol\beta^{*}) = 0, \mathbf{x} \in S \right\}$$ (3.112)

`ovvero il numero degli elementi di $S$ che soddisfano il vincolo espresso da $g$. Il parametro $\boldsymbol\beta^{*}$ che massimizza tale voto è la soluzione statisticamente più probabile al problema.

Sia ora la funzione $p(\mathbf{x}, \boldsymbol\beta)$ un indice di verosimiglianza tra la coppia $(\mathbf{x}, \boldsymbol\beta)$ e il vincolo espresso da $g(\mathbf{x}, \boldsymbol\beta)=0$. La funzione $p$ normalmente è una funzione binaria, ma generalizzando può rappresentare tranquillamente una probabilità. Attraverso la funzione $p$ è possibile costruire la trasformata di Hough $H(\boldsymbol\beta)$ in maniera incrementale attraverso

$$H(\boldsymbol\beta) = \sum_{i=1}^{n} p(\mathbf{x}_i, \boldsymbol\beta)$$ (3.113)

La trasformata di Hough è la somma di tutte queste funzioni.

Per particolari vincoli è possibile semplificare ulteriormente quest'approccio, in modo da ridurre il peso computazionale e l'utilizzo della memoria.

Siano pertanto $\beta_1 \ldots \beta_m$ parametri da stimare, quantizzabili e limitati, e siano $f$ e $\beta_1$ una funzione e un parametro tali che si possa scrivere la funzione $g(\mathbf{x}, \boldsymbol\beta)=0$ come

$$\beta_1 = f(\mathbf{x}, \beta_2 \ldots \beta_m)$$ (3.114)

Se la funzione $g$ è esprimibile come in equazione (3.114), è possibile attraverso il metodo della trasformata di Hough discreta stimare i parametri $\boldsymbol\beta$ che rappresentano il modello più “probabile” fra tutti i punti $\mathbf {x}$ forniti. Per ogni elemento $\mathbf {x}$ è possibile far variare i parametri $\beta_2 \ldots \beta_m$ nel loro intervallo e inserire nell'immagine accumulatore $H(\boldsymbol\beta)$ i valori di $\beta_1$ restituiti dalla funzione (3.114).

In questo modo è possibile generare una mappa n-dimensionale di probabilità usando osservazioni $\mathbf {x}$ affette da rumore e potenzialmente outliers. Allo stesso modo il metodo di Hough permette di stimare un modello in presenza di una mistura di modelli con parametri differenti.

Il metodo di Hough permette prestazioni via via migliori man mano che il numero di vincoli aumenta, limitando dinamicamente per esempio il campo dei parametri associati al campione $\mathbf {x}$. L'algoritmo di Hough può essere visto come una forma degenere di template matching.

Normalmente risulta interessante l'uso di Hough dove il modello ha solo 2 parametri in quanto facilmente graficabile su una mappa bidimensionale.

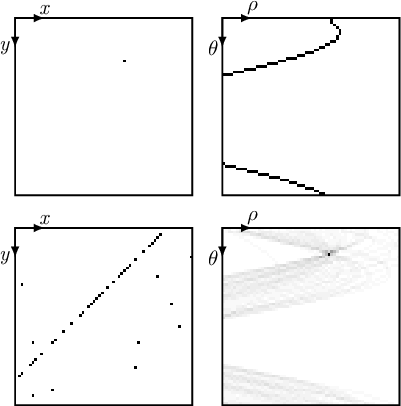
Un esempio molto comune della trasformata di Hough è quello dove $g$ (il modello) è una retta, espressa in forma polare come in equazione (1.46), dove i parametri da ricavare sono $\theta$ e $\rho$: risulta evidente che per ogni coppia di punti $(x,y)$ e per tutti i possibili angoli di $\theta$ quantizzati e limitati (in quanto angolo è un parametro limitato) esiste uno e un solo $\rho$ che soddisfa l'equazione (1.46).

È pertanto possibile creare mappa $H(\theta,\rho)$ dove per ogni punto $(x,y) \in S$ e per ogni $\theta \in [\theta_{min}, \theta_{max}]$ viene incrementata sulla mappa accumulatore l'elemento associato a $(\theta, \cos \theta x + \sin \theta y )$, relazione che soddisfa l'equazione (1.46) della retta scritta sotto forma di coordinate polari.