Regressione lineare a funzione polinomiale

Il metodo applicato per ottenere la regressione lineare a una retta espressa in forma esplicita si può generalizzare a una qualunque funzione polinomiale del tipo:

$$y = \beta_0 + \beta_1 x + \beta_2 x^2 + \ldots + \beta_m x^m + \varepsilon$$ (3.85)

dove $\beta_0 \ldots \beta_m$ sono i parametri della curva da ricavare, parametri che si ottengono cercando il minimo della funzione errore descritta in (3.6). Le derivate di una funzione polinomiale sono notevoli:

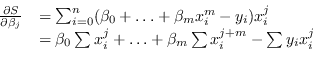$$\begin{array}{rl} \frac{\partial S}{\partial \beta_j} & = ... ...+ \ldots + \beta_m \sum x_i^{j+m} - \sum y_i x_i^j \end{array}$$ (3.86)

Il porre il gradiente nullo significa risolvere pertanto il sistema associato:

$$\begin{bmatrix} \sum 1 & \ldots & \sum x_i^{m} \\ \sum x... ... \sum y_i x_i \\ \vdots \\ \sum y_i x_i^m \\ \end{bmatrix}$$ (3.87)

che è una matrice simmetrica.

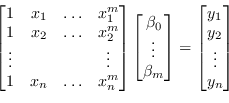
Alternativamente è possibile sfruttare la teoria della pseudoinversa (sezione 1.1) e usare direttamente l'equazione (3.85) per costruire un sistema lineare sovradimensionato:

$$\begin{bmatrix} 1 & x_1 & \ldots & x_1^{m} \\ 1 & x_2 & ... ...bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \\ \end{bmatrix}$$ (3.88)

matrice di Vandermonde. La soluzione di questo sistema permette di ottenere i coefficienti del polinomio che minimizza il quadrato dei residui. Se si pensa alla pseudoinversa risolta con il metodo delle normal equations si vede come il sistema risultante è esattamente lo stesso di equazione (3.87).

Come si vedrà in altre parti di questo libro, matrici come quella di Vandermonde, dove le diverse colonne hanno ordini di grandezza differenti, sono mal condizionate e richiedono una normalizzazione per migliorarne la stabilità numerica.