Il vincolo Soft Margin (4.26) può essere riscritto come
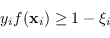 |
(4.37) |
dove
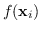 può essere anche la generica funzione kernel.
Questa disequazione è equivalente a
può essere anche la generica funzione kernel.
Questa disequazione è equivalente a
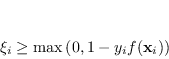 |
(4.38) |
siccome 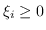 .
La funzione di perdita (4.38) è chiamata funzione perdita cardine (Hinge Loss)
.
La funzione di perdita (4.38) è chiamata funzione perdita cardine (Hinge Loss)
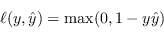 |
(4.39) |
e ha il vantaggio di essere convessa e non differenziabile solo in 1.
La hinge loss è sempre maggiore della funzione perdita 0/1.
Il problema di addestramento di SVM nel caso non linearmente separabile è equivalente a un problema di ottimizzazione, non vincolato, su 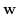 del tipo
del tipo
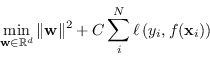 |
(4.40) |
La funzione obiettivo continua ad essere descritta in due parti chiaramente distinte: la prima è la regolarizzazione di Tikhonov e la seconda è la minimizzazione del rischio empirica con la funzione di perdita Cardine.
SVM può essere pertanto visto come un classificatore lineare che ottimizza la funzione di perdita Cardine con una regolarizzazione L2.
I dati di ingresso 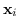 possono cadere in 3 diverse categorie:
possono cadere in 3 diverse categorie:
-
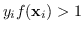 sono i punti fuori dal margine e non danno nessun contributo alla funzione costo;
sono i punti fuori dal margine e non danno nessun contributo alla funzione costo;
-
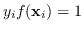 sono i punti sul margine e non danno contributo al costo come nel caso “hard margin”;
sono i punti sul margine e non danno contributo al costo come nel caso “hard margin”;
-
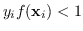 sono i punti che violano il vincolo e contribuiscono al costo.
sono i punti che violano il vincolo e contribuiscono al costo.
Paolo medici
2025-03-12
![]() del tipo
del tipo
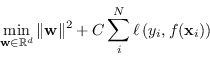
![]() possono cadere in 3 diverse categorie:
possono cadere in 3 diverse categorie: