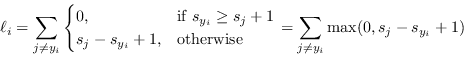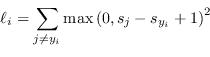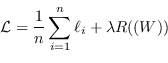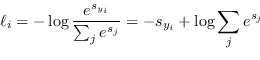SVM ritorna una funzione obiettivo
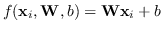 il cui valore assoluto non ha un vero significato in quanto è un uscita non calibrata. L'estensione al caso multiclasse è difficile in quanto le differenti funzioni obiettivo per ogni classe non sono tra loro direttamente confrontabili.
il cui valore assoluto non ha un vero significato in quanto è un uscita non calibrata. L'estensione al caso multiclasse è difficile in quanto le differenti funzioni obiettivo per ogni classe non sono tra loro direttamente confrontabili.
Il concetto di hinge loss può però essere esteso al caso multiclasse. In questo caso viene definita una SVM Loss del tipo
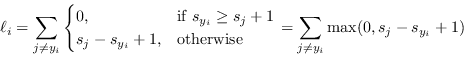 |
(4.41) |
dove con
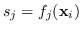 è stato indicato, per semplicità, la funzione obiettivo associato alla classe
è stato indicato, per semplicità, la funzione obiettivo associato alla classe 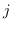 per il campione
per il campione 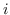 -esimo.
-esimo.
Un'altra metrica simile è la squared hinge loss:
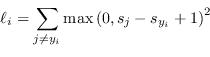 |
(4.42) |
Viene infine definita una funzione perdita sull'intero dataset come media
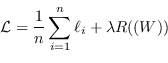 |
(4.43) |
con l'opzionale termine di regolarizzazione sui pesi.
Una metrica differente, estesa al caso multiclasse, è la funzione esponenziale normalizzata Softmax:
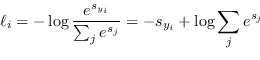 |
(4.44) |
La funzione obiettivo 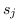 può essere interpretata come una probabilità non normalizzata logaritmica per ogni classe e perciò si può sostituire la funzione perdita cardano con la funzione perdita entropia incrociata (cross-entropy loss).
Un classificatore Softmax minimizza l'entropia incrociata tra le classi e siccome minimizza la negative log likelihood della classe corretta può essere visto come uno stimatore a massima verosimiglianza.
Nel caso Softmax il termine di regolarizzazione
può essere interpretata come una probabilità non normalizzata logaritmica per ogni classe e perciò si può sostituire la funzione perdita cardano con la funzione perdita entropia incrociata (cross-entropy loss).
Un classificatore Softmax minimizza l'entropia incrociata tra le classi e siccome minimizza la negative log likelihood della classe corretta può essere visto come uno stimatore a massima verosimiglianza.
Nel caso Softmax il termine di regolarizzazione 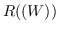 può essere visto, da un punto di vista statistico, come un prior sui pesi: in questo caso è una stima Maximum a posteriori (MAP).
può essere visto, da un punto di vista statistico, come un prior sui pesi: in questo caso è una stima Maximum a posteriori (MAP).
Paolo medici
2025-03-12