Next: Minimizzazione Empirica del Rischio Up: SVM Previous: Soft Margin SVM
Nonostante il Soft Margin, alcuni problemi sono intrinsecamente non separabili nello spazio delle feature.
Tuttavia, dalla conoscenza del problema, è possibile intuire che una trasformazione non lineare ![]() trasforma lo spazio delle feature di input
trasforma lo spazio delle feature di input ![]() nello spazio delle feature
nello spazio delle feature ![]() dove l'iperpiano di separazione permette di discriminare meglio le categorie.
La funzione discriminante nello spazio
dove l'iperpiano di separazione permette di discriminare meglio le categorie.
La funzione discriminante nello spazio ![]() è
è
| (4.30) |
Per permettere la separazione, normalmente lo spazio ![]() è di dimensioni maggiori dello spazio
è di dimensioni maggiori dello spazio ![]() .
Questo aumento di dimensioni provoca un aumento della complessità computazionale del problema e la richiesta di risorse.
I metodi Kernel risolvono questo problema.
.
Questo aumento di dimensioni provoca un aumento della complessità computazionale del problema e la richiesta di risorse.
I metodi Kernel risolvono questo problema.
Il vettore ![]() è una combinazione lineare dei campioni di addestramento (i support vector nel caso hard margin):
è una combinazione lineare dei campioni di addestramento (i support vector nel caso hard margin):
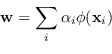 |
(4.31) |
Al momento della valutazione della funzione discriminante pertanto è richiesto l'utilizzo dei vettori di supporto (almeno quelli con un parametro ![]() associato non trascurabile).
Di fatto SVM con kernel individua alcuni campioni dell'insieme di addestramento come informazione utile per capire quanto vicino a loro è il campione di valutazione in esame.
associato non trascurabile).
Di fatto SVM con kernel individua alcuni campioni dell'insieme di addestramento come informazione utile per capire quanto vicino a loro è il campione di valutazione in esame.
Il bias si calcola istantaneamente dall'equazione (4.32), mediando
![\begin{displaymath}
b = \E[ y_j - \sum_i \alpha_i k(\mathbf{x}_j, \mathbf{x}_i) ]
\end{displaymath}](img1157.png) |
(4.33) |
I kernel più diffusi, in quanto semplici da valutare, sono i kernel gaussiani nella forma
| (4.34) |
| (4.35) |
L'utilizzo di funzioni kernel, unita alla possibilità di precalcolare tutte le combinazioni
![]() , permette di definire un'interfaccia comune tra gli addestramenti lineari e i non lineari, mantenendo di fatto lo stesso grado di prestazioni.
, permette di definire un'interfaccia comune tra gli addestramenti lineari e i non lineari, mantenendo di fatto lo stesso grado di prestazioni.
È da notare che le predizione
![]() assume la forma
assume la forma
| (4.36) |
Paolo medici