In applicazioni reali non sempre esiste un margine, ovvero non sempre le classi sono linearmente separabili nello spazio delle features attraverso un iperpiano.
Il concetto alla base del Soft Margin permette di ovviare a questo limite, introducendo una variabile 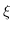 aggiuntiva per ogni campione, in modo da rilassare (slack) il vincolo sul margine
aggiuntiva per ogni campione, in modo da rilassare (slack) il vincolo sul margine
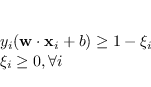 |
(4.26) |
Il parametro 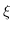 rappresenta la slackness associata al campione.
Quando
rappresenta la slackness associata al campione.
Quando 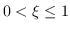 il campione è correttamente classificato ma è all'interno dell'area di margine.
Quando
il campione è correttamente classificato ma è all'interno dell'area di margine.
Quando 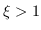 il campione entra nello spazio di decisione della classe opposta e perciò verrà classificato in maniera errata.
il campione entra nello spazio di decisione della classe opposta e perciò verrà classificato in maniera errata.
Per cercare ancora un iperpiano di separazione in qualche modo ottimo, la funzione costo da minimizzare deve considerare anche la distanza tra il campione e il margine:
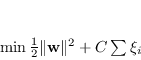 |
(4.27) |
soggetta ai vincoli (4.26).
Il parametro  è un grado di libertà del problema per indicare quanto un campione deve pagare il violare il vincolo sul margine.
Quando
è un grado di libertà del problema per indicare quanto un campione deve pagare il violare il vincolo sul margine.
Quando  è piccolo, il margine è ampio, mentre quando
è piccolo, il margine è ampio, mentre quando  è prossimo a infinito si ricade alla formulazione Hard Margin di SVM vista in precedenza.
è prossimo a infinito si ricade alla formulazione Hard Margin di SVM vista in precedenza.
Ogni campione 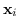 può ricadere in uno di tre possibili stati:
può ricadere in uno di tre possibili stati:
- può stare oltre il margine
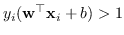 e di conseguenza non contribuire alla funzione;
e di conseguenza non contribuire alla funzione;
- può stare sul margine
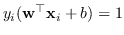 non partecipando direttamente alla minimizzazione ma solo come support vector,
non partecipando direttamente alla minimizzazione ma solo come support vector,
- può infine cadere all'interno del margine ed essere penalizzato tanto quanto si discosta dai vincoli forti.
La lagrangiana del sistema (4.27), con i vincoli introdotti dalle variabili 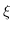 , è
, è
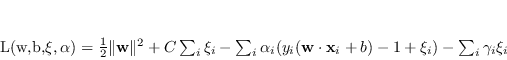 |
(4.28) |
Con l'aumento del numero di vincoli, le variabili duali sono sia 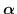 che
che 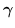 .
.
Il risultato notevole è che, applicate le derivate, la formulazione duale di (4.28) diventa esattamente uguale alla duale del caso Hard Margin:
le variabili 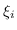 infatti non compaiono nella formulazione duale
e l'unica differenza tra il caso Hard Margin e il caso Soft Margin è nel vincolo sui parametri
infatti non compaiono nella formulazione duale
e l'unica differenza tra il caso Hard Margin e il caso Soft Margin è nel vincolo sui parametri 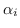 , in questo caso limitati tra
, in questo caso limitati tra
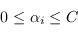 |
(4.29) |
invece che con la semplice diseguaglianza
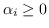 .
Il grande vantaggio di questa formulazione è proprio nella elevata semplicità dei vincoli e nel fatto che permetta di ricondurre il caso Hard Margin a un caso particolare (
.
Il grande vantaggio di questa formulazione è proprio nella elevata semplicità dei vincoli e nel fatto che permetta di ricondurre il caso Hard Margin a un caso particolare (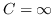 ) del Soft Margin.
La costante
) del Soft Margin.
La costante  è un limite superiore al valore che gli
è un limite superiore al valore che gli 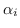 possono assumere.
possono assumere.
Paolo medici
2025-03-12
![]() può ricadere in uno di tre possibili stati:
può ricadere in uno di tre possibili stati:
![]() , è
, è
![]() infatti non compaiono nella formulazione duale
e l'unica differenza tra il caso Hard Margin e il caso Soft Margin è nel vincolo sui parametri
infatti non compaiono nella formulazione duale
e l'unica differenza tra il caso Hard Margin e il caso Soft Margin è nel vincolo sui parametri ![]() , in questo caso limitati tra
, in questo caso limitati tra