Next: Auto-Encoders Up: Apprendimento Profondo Previous: Representation learning
Il punto di rottura tra le tecniche non profonde e le tecniche profonde di addestramento è considerato il 2006 quando Hinton e altri all'University of Toronto introducono le Deep Belief Networks (DBNs) (HOT06), un algoritmo che “avidamente” addestra una struttura a strati addestrando uno strato alla volta sfruttando un algoritmo di addestramento non-supervisionato. La peculiarità delle DBN consiste nel fatto che gli strati sono costituiti da Restricted Boltzmann Machine (RBM) (FH94,Smo86).
Sia
![]() una variabile stocastica binaria associata allo stato visibile e
una variabile stocastica binaria associata allo stato visibile e
![]() una variabile stocastica binaria associata allo stato nascosto.
Dato uno stato
una variabile stocastica binaria associata allo stato nascosto.
Dato uno stato
![]() l'energia della configurazione degli strati visibili e nascosti è data da (Hop82)
l'energia della configurazione degli strati visibili e nascosti è data da (Hop82)
La probabilità della configurazione congiunta
![]() è data dalla distribuzione di Boltzmann:
è data dalla distribuzione di Boltzmann:
La parola restricted fa riferimento al fatto che non sono ammesse interazioni diretta tra le unità appartenenti allo stesso strato ma solo tra strati limitrofi.
Dato un input ![]() , lo stato binario nascosto
, lo stato binario nascosto ![]() viene attivato con probabilità:
viene attivato con probabilità:
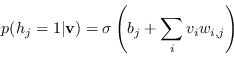 |
(4.85) |
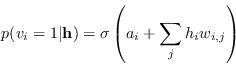 |
(4.86) |
Ottenere il modello
![]() che permetta di rappresentare tutti i valori di ingresso in addestramento è un compito tuttavia molto complesso.
Una procedura molto più veloce è stata proposta da Hinton nel 2002: solo da quel momento infatti le RBM possono venire addestrate con l'algoritmo di contrastive divergence (CD) (Hin12).
che permetta di rappresentare tutti i valori di ingresso in addestramento è un compito tuttavia molto complesso.
Una procedura molto più veloce è stata proposta da Hinton nel 2002: solo da quel momento infatti le RBM possono venire addestrate con l'algoritmo di contrastive divergence (CD) (Hin12).
Paolo medici