Next: Feature di Haar Up: Elementi di analisi per Previous: AST
Un altro concetto che ha una collocazione trasversale tra le tematiche di visione artificiale è quello di descrittore (Visual Descriptor). Il descrittore infatti viene usato in diverse tematiche: viene usato per eseguire il confronto tra punti caratteristici o per generare la mappa di disparità nella visione stereoscopia, per fornire una rappresentazione compatta di una porzione dell'immagine per velocizzare la sua individuazione o ricerca, e grazie a questa soluzione compatta che però preserva gran parte dell'informazione, viene usata per generare lo spazio delle caratteristiche negli algoritmi di classificazione.
A seconda della trasformazione che subisce l'immagine da cui si vogliono caratterizzare i punti, il descrittore deve soddisfare alcuni principi di invarianza
Prima che venisse introdotto il concetto di descrittore compatto, il modo universalmente diffuso per confrontare due punti caratteristici era la correlazione tra le aree intorno al punto:
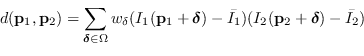 |
(6.1) |
Un approccio simile alla correlazione, non invariante alla luminosità ma più performante dal punto di vista computazionale, è la SAD (Sum of Absolute Differences):
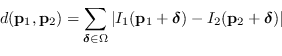 |
(6.2) |
É altresı da notare che il confronto tra i pixel tra le immagini è comunque un algoritmo di tipo ![]() : eseguire questi confronti per punto richiede comunque un elevato peso computazionale e molteplici accessi in memoria.
Soluzioni moderne vogliono superare questo limite prevedendo l'estrazione di un descrittore dall'intorno del punto di dimensione inferiore alla quantità di pixel rappresentati che però massimizzi l'informazione contenuta in essa.
: eseguire questi confronti per punto richiede comunque un elevato peso computazionale e molteplici accessi in memoria.
Soluzioni moderne vogliono superare questo limite prevedendo l'estrazione di un descrittore dall'intorno del punto di dimensione inferiore alla quantità di pixel rappresentati che però massimizzi l'informazione contenuta in essa.
Sia SIFT (sezione 5.3) che SURF (sezione 5.4) estraggono i loro descrittori sfruttando le informazioni sulla scala e sulla rotazione estratti dall'immagine (é possibile estrarre queste informazioni in maniera comunque indipendete e pertanto si possono applicare a qualunque classe di descrittori per renderli invarianti a scala e rotazione). I descrittori ottenuti da SIFT e SURF, sono differenti versioni del medesimo concetto, ovvero dell'istogramma dell'orientazione del gradiente (sezione 6.2), esempio di come comprimere in uno spazio di dimensioni ridotte la variabilità intorno al punto.
Tutti i descrittori usati attualmente non usano direttamente i punti dell'immagine come descrittore, ma è facile vedere che basta un sottoinsieme abbastanza ben distribuito dei punti per realizzare comunque una descrizione accurata del punto. In (RD05) viene creato un descrittore con i 16 pixel presenti lungo la circonferenza discreta di raggio 3. Tale descrizione può essere resa ancora più compatta passando alla forma binaria dei Local Binary Pattern descritti in seguito o non vincolata alla circonferenza, come in Census o in BRIEF.
Un altro approccio è campionare in maniera opportuna lo spazio dei kernel (GZS11), estraendo da ![]() coordinate intorno al punto chiave, i valori che assumono convoluzioni dell'immagine originale (Sobel orizzontale e verticale), in modo da creare un descrittore di appena
coordinate intorno al punto chiave, i valori che assumono convoluzioni dell'immagine originale (Sobel orizzontale e verticale), in modo da creare un descrittore di appena ![]() valori.
valori.
É da notare che, per motivi prettamente computazionali di riutilizzo di risorse, spesso ad ogni particolare estrattore di punti caratteristici viene associato uno specifico estrattore di descrittori.
Da questa introduzione si capisce che descrivere un punto chiave con un insieme di dati inferiore ma allo stesso tempo sufficientemente descrittivo è un discorso che torna utile anche quando si parla di classificazione. Il concetto di descrittore nasce nel tentativo di estrarre informazioni locali dell'immagine che ne permettano di conservare buona parte dell'informazione. In questo modo è possibile eseguire confronti (relativamente) veloci tra punti tra immagini, o usare tali descrittori come caratteristiche su cui addestrare classificatori.