Next: AST Up: Punti Caratteristici Previous: Invarianza alla scala e
L'algoritmo Speeded Up Robust Features (BETVG08) prende spunto dall'algoritmo SIFT e dalla teoria delle rappresentazioni scala-spazio per proporne una versione ottimizzata dove si sfruttano hessiane approssimate utilizzando l'immagine integrale, sia per individuare i punti caratteristici che per estrarne i descrittori.
SURF è invariante alla traslazione, scala e rotazione ma esiste una variante semplificata, indicata con “U-SURF”, che è solo invariante a variazioni di traslazione e scala: in questo caso l'area intorno al punto individuato non viene normalizzata rispetto alla rotazione nel momento in cui viene estratto il descrittore.
In SURF i punti caratteristici vengono rilevati calcolando massimi locali sul determinante dell'immagine Hessiana definita come:
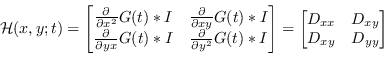 |
(5.13) |
La banda di questi filtri approssimati si può stimare come
| (5.14) |
L'immagine determinante viene calcolata come
| (5.15) |
L'immagine viene analizzata per più ottave (ogni ottava ha un fattore di scala doppio rispetto all'ottava precedente). Ogni ottava è divisa in un ugual numero di livelli di scala. Il numero di scale per ottava è limitato dalla natura strettamente quantizzata del filtro e le gaussiane approssimate non sono ben equispaziate come nel caso di SIFT. Di fatto 4 intervalli per ottava è l'unico numero di suddivisioni possibile.
All'interno di ogni ottava, al variare della scala ![]() e della posizione, viene eseguita una Non-Maxima Suppression
e della posizione, viene eseguita una Non-Maxima Suppression
![]() sull'immagine del determinante di
sull'immagine del determinante di ![]() .
I minimi/massimi locali, interpolati attraverso una quadrica tridimensionale come per SIFT, sono i punti interessanti individuati da SURF.
La scala è posta uguale alla varianza del filtro associato
.
I minimi/massimi locali, interpolati attraverso una quadrica tridimensionale come per SIFT, sono i punti interessanti individuati da SURF.
La scala è posta uguale alla varianza del filtro associato ![]() .
.
Dai punti di massimo cosı trovati, usando sempre l'immagine integrale, viene estratta l'orientazione dominante nell'intorno del punto (intorno di raggio ![]() e campionato a passo
e campionato a passo ![]() ).
Anche questo caso vengono usate feature di Haar di lato
).
Anche questo caso vengono usate feature di Haar di lato ![]() e pesate con una gaussiana di distribuzione
e pesate con una gaussiana di distribuzione ![]() .
.
Attraverso l'informazione sull'orientazione viene generato un descrittore basato sulle direzioni dei gradienti campionando l'area in un intorno di ![]() , divisa in
, divisa in ![]() regioni e pesando i punti con una gaussiana
regioni e pesando i punti con una gaussiana ![]() . All'interno di ogni regione vengono calcolati
. All'interno di ogni regione vengono calcolati ![]() ,
, ![]() ,
, ![]() e
e ![]() .
Sia l'orientazione che l'istogramma dei gradienti sono estratti alla scala di rilevamento della feature.
.
Sia l'orientazione che l'istogramma dei gradienti sono estratti alla scala di rilevamento della feature.
Paolo medici