Invarianza alla scala e alla rotazione

Harris è un individuatore di punti notevoli non invariante alle variazioni di scala. Per superare questa serie di limiti, Lindeberg (Lin14,Lin94) introduce il concetto di selezione automatica della scala, permettendo di individuare i punti caratteristici a un determinato livello di risoluzione. La rappresentazione piramidale della scena, algoritmo computazionalmente efficiente ampiamente usato in precedenza, diventa di fatto un caso particolare di questa rappresentazione scala-spazio.

Sia $G(x,y;t)$ la gaussiana bidimensionale di varianza $t > 0$, di equazione

$$G(x,y;t) = \frac{1}{2\pi t} e^{-\frac{x^{2}+y^{2}}{2t} }$$ (5.7)

(cfr. sezione 2.2).

La convoluzione $L(x,y;t)$ tra l'immagine $I(x,y)$ e la gaussiana $G(x,y;t)$

$$L(x,y;t) = G(x,y;t) \ast I(x,y)$$ (5.8)

genera la rappresentazione scala-spazio (scale-space representation) dell'immagine stessa. La varianza $t=\sigma^2$ del kernel gaussiano è chiamata parametro di scala (scale parameter). La rappresentazione dell'immagine alla scala degenere $t=0$ è l'immagine originale stessa.

È da notare che applicare un filtro gaussiano a un immagine non crea nuove strutture: tutta l'informazione generata dal filtro era già contenuta nell'immagine originale.

Figura 5.2: Rappresentazione scala-spazio di una immagine $512 \times 512$: dall'immagine originale $t=0$ alle scale 1, 4, 16, 64 e 256.

Il fattore di scala $t$ è un numero continuo ma, per motivi computazionali, vengono usati passi discreti di questo valore, normalmente successioni esponenziali, come $t=2^i$ o $t=\frac{1}{2} e^{i}$.

Applicare a una immagine scala-spazio un operatore derivata, per la proprietà commutativa tra la convoluzione e la derivata, è uguale ad eseguire la convoluzione dell'immagine originale con la derivata della gaussiana:

$$L_{x^{\alpha}}(\cdot ; t) = \partial_{x^{\alpha}}L(\cdot; t) = (\partial_{x^{\alpha}} g(\cdot; t) ) \ast f(\cdot)$$ (5.9)

con $\alpha$ notazione multi-indice della derivata. Allo steso modo è possibile estendere a un qualsiasi fattore di scala la definizione di tutti i filtri bordo o punti caratteristici. Attraverso il lavoro di Lindeberg è stato possibile estendere il concetto dei Corner di Harris a casi invarianti di scala (metodi Harris-Laplace e Hessian-Laplace (MS02)).

Alcuni operatori interessanti per trovare punti caratteristici sono per esempio il modulo del gradiente $\vert\nabla L\vert$, il laplaciano $\nabla^{2} L$ e il determinante dell'hessiana $\det \mathcal{H}(L)$. Tutti questi operatori sono invarianti alle rotazioni, ovvero il punto di minimo/massimo esiste indipendentemente dalla rotazione che assume l'immagine.

Tra questi operatori, uno molto diffuso per individuare punti caratteristici è il Laplaciano della Gaussiana (LoG) normalizzato (scale-normalized Laplacian operator):

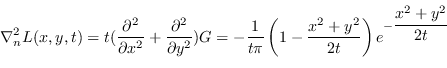$$\nabla_{n}^{2} L(x,y,t) = t(\frac{\partial^2}{\partial x^{... ... 1 - \frac{x^2 + y^2}{2t} \right) e^{-\dfrac{x^2 + y^2}{2t} }$$ (5.10)

Attraverso l'operatore LoG, è possibile individuare punti caratteristici come massimi o minimi locali nelle coordinate spaziali e scala.

Per esempio, un cerchio di raggio $r$ ha la massima risposta al laplaciano al fattore di scala $\sigma = r / \sqrt{2}$.

Figura 5.3: Confronto tra l'immagine LoG normalizzata (a) e DoG (b)

(a)	(b)

Lowe (Low04), nell'algoritmo Scale-invariant feature transform (SIFT), per aumentare le prestazioni, approssima il Laplaciano della Gaussiana (LoG) con una Differenza tra Gaussiane (DoG):

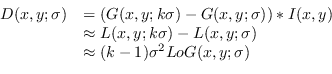$$\begin{array}{rl} D(x,y;\sigma) & = (G(x,y;k\sigma ) - G(... ... \\ & \approx (k-1) \sigma^2 LoG(x,y;\sigma) \end{array}$$ (5.11)

Questo procedimento è più performante in quanto l'immagine gaussiana a scala $k\sigma$ può venire calcolata dall'immagine gaussiana $\sigma$ applicando un filtro $(k-1)\sigma$, più piccolo e perciò nel complesso molto più veloce rispetto ad eseguire la convoluzione $k\sigma$ con l'immagine originale.

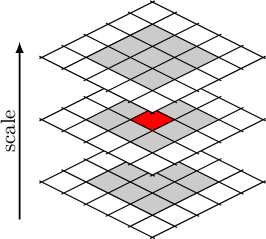
Se in LoG i punti caratteristici erano i minimi/massimi locali, sia nello spazio che nella scala, dell'immagine del laplaciano, in questo caso i punti caratteristici sono i punti minimo e massimo nell'immagine differenza tra le immagini scala $\sigma, k\sigma, \ldots, k^n\sigma$ attraverso le quali viene processata l'immagine (figura 5.4).

Figura 5.4: Individuazione di minimi e massimi locali: per ogni pixel e per ogni scala viene confrontato un intorno $3\times 3\times 3$.

Con l'introduzione del passo $k$, il dominio della variabile $\sigma$ viene di fatto suddiviso in passi logaritmici discreti, raccolti in ottave, e ogni ottava viene suddivisa in $S$ sottolivelli. In questo modo $\sigma$ assume i valori discreti

$$\sigma(o,s) = \sigma_0 2^{o + \frac{s}{S}} \leftrightarrow k=2^{\frac{1}{S}}$$ (5.12)

con $\sigma_0$ fattore base di scala.

I punti caratteristici, trovati come massimo/minimo in scala e spazio, entrambi discreti, vengono interpolati usando una regressione a una quadrica tridimensionale per trovare il punto caratteristico con precisione subpixel e subscala.

Tra un ottava e quella successiva l'immagine viene sottocampionata di un fattore 2: oltre all'analisi a scale multiple all'interno di ogni ottava, l'immagine viene processata nuovamente nell'ottava successiva dimezzando la dimensione orizzontale e verticale e tale procedimento viene ripetuto più volte.

La seconda fase di un algoritmo di individuazione e associazione di punti caratteristici consiste nell'estrarre un descrittore per eseguire i confronti, descrittore centrato nel punto caratteristico individuato. Di fatto, per essere invariante alla scala il descrittore deve essere estratto al medesimo fattore di scala associato al punto caratteristico.

Per essere invariante invece alla rotazione il descrittore deve essere estratto da una immagine che ha subito una qualche forma di normalizzazione rispetto alla direzione dominante estratta in intorno del punto valutato.

Da questa immagine ruotata alla scala del punto caratteristico è possibile estrare un descrittore che da importanza ai bordi nell'intorno per essere infine inviariante alla luminosità.

Tra le innumerevoli varianti va segnalato PCA-SIFT che usa PCA per ridurre le dimensioni del problema a un descrittore di soli 36 elementi. PCA viene usato in una fase precedente di addestramento.