Next: Invarianza alla scala e Up: Punti Caratteristici Previous: Individuatore Hessiano
L'algoritmo di Förstner-Harris (HS88,FG87) è stato esplicitamente disegnato per ottenere una elevata stabilità geometrica. Esso definisce punti caratteristici quei punti che hanno un massimo locale nel confronto ai minimi quadrati alla propria versione sottoposta a traslazione. Questo algoritmo ha avuto così tanto successo perchè permette di individuare le variazione dell'intensità dell'immagine nell'intorno di un punto usando la matrice di auto-correlazione tra le derivate prime dell'immagine.
Si definiscano le immagini dei gradienti (queste possono essere generate da un operatore differenziale, Sobel, Prewit o Roberts) ![]() e
e ![]() rispettivamente gradiente orizzontale e gradiente verticale dell'immagine da analizzare.
rispettivamente gradiente orizzontale e gradiente verticale dell'immagine da analizzare.
Da queste due immagini è possibile calcolare una funzione
![]() , rappresentate la matrice di covarianza (autocorrelazione) delle immagini dei gradienti in un intorno di
, rappresentate la matrice di covarianza (autocorrelazione) delle immagini dei gradienti in un intorno di ![]() , definita come
, definita come
Di fatto in Harris si usano due filtri di convoluzione: uno derivativo per calcolare le immagini derivate e uno integrale per calcolare gli elementi della matrice. La dimensione di questi filtri e l'utilizzo di filtro gaussiano per pesare i punti rimanda alla lettura della sezione seguente riguardo la scala di individuazione delle feature.
La matrice ![]() è la matrice dei momenti del secondo ordine.
Per individuare punti caratteristici si possono analizzare gli autovalori
è la matrice dei momenti del secondo ordine.
Per individuare punti caratteristici si possono analizzare gli autovalori ![]() e
e ![]() della matrice
della matrice ![]() (si legga per una trattazione più approfondita la sezione 2.10.1).
Gli autovalori della matrice di auto-correlazione
(si legga per una trattazione più approfondita la sezione 2.10.1).
Gli autovalori della matrice di auto-correlazione ![]() permettono di caratterizzare il tipo di immagine contenuta nella finestra intorno al punto dato.
permettono di caratterizzare il tipo di immagine contenuta nella finestra intorno al punto dato.
Se sono presenti due autovalori molto elevati il punto è un corner, se è presente un solo autovalore di valore elevato è un edge, altrimenti è una zona ragionevolmente piatta, ovvero in forma di funzione come
| (5.4) |
Per una matrice ![]() gli autovalori si ottengono come soluzioni del polinomio caratteristico quadratico
gli autovalori si ottengono come soluzioni del polinomio caratteristico quadratico
| (5.5) |
Harris, per evitare di calcolare esplicitamente gli autovalori di ![]() , introduce un operatore
, introduce un operatore ![]() definito come
definito come
| (5.6) |
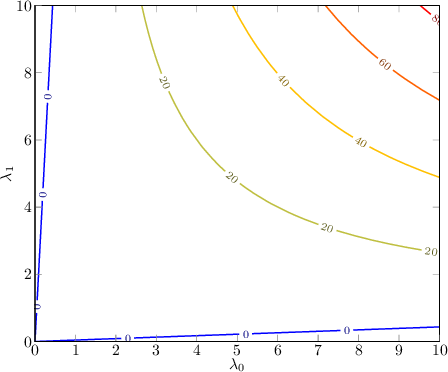 |
Per Harris il punto ![]() è un punto caratteristico (corner) se
è un punto caratteristico (corner) se
![]() , con
, con ![]() soglia da definire.
Il parametro
soglia da definire.
Il parametro ![]() regola la sensitività del rilevatore di feature.
Qualitativamente alzare
regola la sensitività del rilevatore di feature.
Qualitativamente alzare ![]() rimuove i bordi mentre alzare
rimuove i bordi mentre alzare ![]() rimuove le zone piatte (figura 5.1).
rimuove le zone piatte (figura 5.1).
Paolo medici