Next: Calcolo MLE dell'omografia Up: Calibrazione Previous: Calibrazione
L'idea base della Direct Linear Transformation proposta da Abdel-Aziz e Karara (AAK71) permette di calcolare direttamente i coefficienti delle matrici (8.50), (8.53) o della matrice (8.18) disinteressandosi completamente dei parametri e dalla struttura del modello della trasformazione prospettica. In tale articolo viene anche presentato un approccio per risolvere problemi sovradimensionati attraverso la tecnica della Pseudoinversa.
Dato il sistema (8.18) è necessario ricavare i 12 parametri della matrice proiettiva ![]() per avere una calibrazione del sistema implicita ovvero dove non si conoscono i parametri (da 9 a 11 a seconda del modello) interni che han generato gli elementi della matrice stessa. Tale rappresentazione della camera pin-hole è ovviamente ideale (senza non-linearità dal modello).
per avere una calibrazione del sistema implicita ovvero dove non si conoscono i parametri (da 9 a 11 a seconda del modello) interni che han generato gli elementi della matrice stessa. Tale rappresentazione della camera pin-hole è ovviamente ideale (senza non-linearità dal modello).
La funzione prospettica scritta in forma implicita è
Essendo un sistema omogeneo, la sua soluzione sarà il sottospazio nullo di
![]() , kernel della matrice dei termini noti. Per questo motivo la matrice
, kernel della matrice dei termini noti. Per questo motivo la matrice ![]() è conosciuta a meno di un fattore moltiplicativo e ne consegue che ha solo 11 parametri liberi (sono anche di meno considerando che una telecamera moderna ha solo 3-4 parametri intrinseci e i 6 estrinseci).
Avendo rigirato il sistema la propagazione del rumore sui punti non è più lineare e questa soluzione non soddisfa la massima verosimiglianza.
La matrice
è conosciuta a meno di un fattore moltiplicativo e ne consegue che ha solo 11 parametri liberi (sono anche di meno considerando che una telecamera moderna ha solo 3-4 parametri intrinseci e i 6 estrinseci).
Avendo rigirato il sistema la propagazione del rumore sui punti non è più lineare e questa soluzione non soddisfa la massima verosimiglianza.
La matrice ![]() ottenuta attraverso questo procedimento, anche se nasconde la struttura interna del sensore, permette di proiettare un punto da coordinate mondo a coordinate immagine e da un punto in coordinate immagine ricavare la retta che sottende tale punto nel mondo.
ottenuta attraverso questo procedimento, anche se nasconde la struttura interna del sensore, permette di proiettare un punto da coordinate mondo a coordinate immagine e da un punto in coordinate immagine ricavare la retta che sottende tale punto nel mondo.
Il risultato è generalmente instabile usando solo 6 punti e perciò la stima viene normalmente effettuata processando più punti del minimo e si sfruttano tecniche come la pseudoinversa per determinare una soluzione che minimizzi gli errori di misura.
Il problema è uguale a quello visto in precedenza, la soluzione omogenea esiste e l'equazione risolutiva omogenea (8.47) si generalizza in
Questa formulazione è utile quando il modello proiettivo non segue il modello pin-hole ma è sempre possibile ricavare le coordinate “camera” dei raggi ottici sottesi al pixel e pertanto disponibili in formato omogeneo.
Solitamente per ridurre il numero di elementi della matrice ![]() si può aggiungere il vincolo che tutti i punti coinvolti nel processo di calibrazione appartengano a un piano particolare (per esempio al terreno).
Ciò significa porre la condizione
si può aggiungere il vincolo che tutti i punti coinvolti nel processo di calibrazione appartengano a un piano particolare (per esempio al terreno).
Ciò significa porre la condizione ![]()
![]() , che implica l'eliminazione di una colonna (relativa all'asse
, che implica l'eliminazione di una colonna (relativa all'asse ![]() ) della matrice
che si riduce alla dimensione
) della matrice
che si riduce alla dimensione ![]() , diventa invertibile e si può definire omografica (vedi sezione 1.10).
, diventa invertibile e si può definire omografica (vedi sezione 1.10).
Definiamo pertanto la matrice
![]() (crf. con (8.30)) come
(crf. con (8.30)) come
Come nel caso precedente è possibile trasformare la relazione non lineare (8.50) in modo da ottenere dei vincoli lineari:
Se si dispone di un risolutore di sistemi lineari abbastanza moderno il vincolo aggiuntivo
![]() è automaticamente soddisfatto durante il calcolo del kernel della matrice dei termini noti (fattorizzazione QR o decomposizione SVD).
è automaticamente soddisfatto durante il calcolo del kernel della matrice dei termini noti (fattorizzazione QR o decomposizione SVD).
Un altro metodo più semplice ed intuivo consiste nel porre come vincolo aggiuntivo ![]() : in questo modo, invece che risolvere un sistema omogeneo, si può risolvere un problema lineare tradizionale.
Il sistema (8.50) si può anche in questo caso riarrangiare in modo da ottenere dei vincoli lineari nella forma:
: in questo modo, invece che risolvere un sistema omogeneo, si può risolvere un problema lineare tradizionale.
Il sistema (8.50) si può anche in questo caso riarrangiare in modo da ottenere dei vincoli lineari nella forma:
L'avere imposto ![]() tuttavia implica che il punto
tuttavia implica che il punto ![]() non può essere una singolarità dell'immagine (es. linea dell'orizzonte), e in generale
non è una scelta ottima dal punto di vista della precisione della soluzione come già discusso in precedenza.
non può essere una singolarità dell'immagine (es. linea dell'orizzonte), e in generale
non è una scelta ottima dal punto di vista della precisione della soluzione come già discusso in precedenza.
È importante notare che la soluzione dipende fortemente dalla normalizzazione scelta. La scelta ![]() può essere chiamata standard least-squares.
può essere chiamata standard least-squares.
In entrambi i casi sono richiesti almeno 4 punti per ottenere un omografia ![]() e ogni punto in più permette di ottenere una soluzione di errore inferiore.
Questi sistemi, quando sovradimensionati, possono essere risolti usando il metodo della pseudoinversa 1.1.
e ogni punto in più permette di ottenere una soluzione di errore inferiore.
Questi sistemi, quando sovradimensionati, possono essere risolti usando il metodo della pseudoinversa 1.1.
La matrice ![]() è definita da 4 parametri intrinseci e dai 6 parametri estrinseci.
La separazione dei parametri intrinseci dai parametri estrinseci suggerisce di estrarre tali parametri in maniera indipendente in modo da irrobustire la calibrazione.
Dopotutto i parametri intrinseci possono essere ricavati con un certo grado di precisione offline e valgono per tutti i possibili posizionamenti della camera (si veda poi 8.5.4).
è definita da 4 parametri intrinseci e dai 6 parametri estrinseci.
La separazione dei parametri intrinseci dai parametri estrinseci suggerisce di estrarre tali parametri in maniera indipendente in modo da irrobustire la calibrazione.
Dopotutto i parametri intrinseci possono essere ricavati con un certo grado di precisione offline e valgono per tutti i possibili posizionamenti della camera (si veda poi 8.5.4).
Definiamo la matrice
![]() (cfr. con (8.31)) come
(cfr. con (8.31)) come
La matrice ![]() è definita a meno di un fattore di scala, mentre
è definita a meno di un fattore di scala, mentre
![]() permette di definire la scala in quanto presenta ancora due colonne ortonormali.
La conoscenza delle due colonne della matrice di rotazione permette di ricavare la terza e perciò tale calibrazione diventa valida per punti anche fuori dal piano
permette di definire la scala in quanto presenta ancora due colonne ortonormali.
La conoscenza delle due colonne della matrice di rotazione permette di ricavare la terza e perciò tale calibrazione diventa valida per punti anche fuori dal piano ![]() .
.
Come è stato fatto in precedenza, un sistema non-lineare in 3 equazioni omogenee, quando opportunamente riarrangiato, fornisce due vincoli lineari:
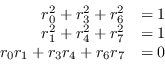 |
(8.55) |
Le equazioni (8.47) e (8.51) si possono ricavare anche da considerazioni puramente geometriche in quanto i vettori immagine e camera devono essere paralleli (il fattore ![]() è puramente moltiplicativo e sul vettore al massimo incide una trasformazione affine):
è puramente moltiplicativo e sul vettore al massimo incide una trasformazione affine):
| (8.56) |
Paolo medici