Next: Calibrazione con il metodo Up: Calibrazione Previous: Calcolo MLE dell'omografia
La calibrazione della camera per diverse applicazioni richiede la conoscenza completa dei parametri intrinseci ed estrinseci. Uno dei metodi più diffusi è sicuramente quello di Tsai (Tsa87) del 1985. Il pregio di Tsai è stato quello di dare ordine allo stato dell'arte discusso in precedenza e fornire una nomenclatura unica ed accettata per i parametri della camera come qui presentati.
Il modello della camera di Tsai è basato sulla proiezione prospettica della Pin-Hole Camera, ed è formato (nella sua forma classica) da 11 parametri:
Tsai esegue sia una analisi di tutte le tecniche sviluppate finora per la calibrazione, e infine propone un sistema a moduli, dove ogni modulo permette di ricavare una serie di questi parametri.
Principalmente fa notare che se la camera è distorta ma si pone il principal point coincidente con il centro di distorsione valgono i rapporti:
| (8.65) |
Inizialmente usando i parametri della camera forniti dal produttore calcola il vettore traslazione e rotazione da una griglia con punti coplanari ![]() di coordinate note, sfruttando il vincolo
di coordinate note, sfruttando il vincolo
| (8.66) |
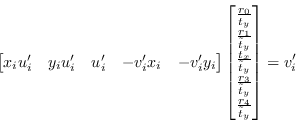 |
(8.67) |
Successivamente procede nel ricavare i parametri intrinseci corretti usando questi valori per la matrice di rotazione e traslazione.
Paolo medici