Next: Il problemi P3P e Up: Calibrazione Previous: Calibrazione secondo Tsai
Zhang (Zha99) e contemporaneamente Sturm e Maybank (SM99) individuano un metodo per ottenere una equazione lineare per ricavare i parametri della camera, eseguendo anche un aggiornamento delle tecniche di calibrazione (sempre valide, ma ormai relative agli anni 80) fatte principalmente da Tsai (Tsa87) e altri (WM94).
Questa tecnica sfrutta il calcolo di diverse matrici omografiche ![]() ottenute dall'osservazione di un piano (per esempio una griglia di calibrazione con marker equispaziati) e da queste cerca di ricavare i parametri intrinseci della camera in maniera esplicita. Come già discusso in precedenza la matrice
ottenute dall'osservazione di un piano (per esempio una griglia di calibrazione con marker equispaziati) e da queste cerca di ricavare i parametri intrinseci della camera in maniera esplicita. Come già discusso in precedenza la matrice ![]() , trasformazione omografica di un piano, possiede 8 gradi di libertà ma non è possibile direttamente ricavare i 10 parametri espliciti che l'hanno generata.
Metodi per ottenere la matrice omografica date le corrispondenze tra punti immagine e punti del piano sono discussi in sezione 8.5.1.
, trasformazione omografica di un piano, possiede 8 gradi di libertà ma non è possibile direttamente ricavare i 10 parametri espliciti che l'hanno generata.
Metodi per ottenere la matrice omografica date le corrispondenze tra punti immagine e punti del piano sono discussi in sezione 8.5.1.
La matrice ![]() e in particolare l'equazione (8.30) può essere esplicitata come
e in particolare l'equazione (8.30) può essere esplicitata come
Nonostante la presenza del fattore ![]() è infatti possibile esprimere delle relazioni basate sull'ortogonalità tra i vettori
è infatti possibile esprimere delle relazioni basate sull'ortogonalità tra i vettori ![]() e
e ![]() in modo da forzare i seguenti due vincoli:
in modo da forzare i seguenti due vincoli:
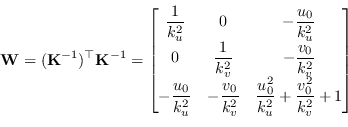 |
(8.70) |
Le 4 (o 5 incognite non trascurando lo skew) della matrice ![]() sotto i 2 vincoli (8.69) possono essere risolte usando almeno 2 (o 3) piani diversi, ovvero matrici
sotto i 2 vincoli (8.69) possono essere risolte usando almeno 2 (o 3) piani diversi, ovvero matrici ![]() le cui colonne non siano linearmente dipendenti tra loro.
le cui colonne non siano linearmente dipendenti tra loro.
Ottenuta la matrice ![]() , con la decomposizione di Cholesky si può determinare infine la matrice originale.
Alternativamente Zhang fornisce le equazioni per ottenere i parametri intrinseci della camera direttamente dalla matrice
, con la decomposizione di Cholesky si può determinare infine la matrice originale.
Alternativamente Zhang fornisce le equazioni per ottenere i parametri intrinseci della camera direttamente dalla matrice ![]() .
Si può infatti trasformare
.
Si può infatti trasformare
![]() ,
con opportuni valori del vettore
,
con opportuni valori del vettore
![]() e con
e con ![]() , vettore da determinare, con i valori non nulli della matrice triangolare superiore di
, vettore da determinare, con i valori non nulli della matrice triangolare superiore di ![]() . In questo modo il sistema di equazioni (8.69) si trasforma nella soluzione di un sistema lineare omogeneo in
. In questo modo il sistema di equazioni (8.69) si trasforma nella soluzione di un sistema lineare omogeneo in ![]() .
.
Determinati i parametri intrinseci e la matrice ![]() , per ogni matrice omografica
, per ogni matrice omografica ![]() usata nella fase di ottimizzazione è possibile stimare la rotazione e la traslazione:
usata nella fase di ottimizzazione è possibile stimare la rotazione e la traslazione:
| (8.71) |
Il sistema nel suo complesso è comunque mal condizionato e difficilmente si giunge a una soluzione stabile dopo ripetute prove. I valori ottenuti attraverso questa tecnica lineare servono però come punto di inizio in una fase di Maximum Likelihood Estimation per minimizzare gli errori di riproiezione (sezione 8.5.6).
Una sola nota: Zhang nel suo articolo fa coincidere il Principal Point con il centro di distorsione, cosa generalmente non esatta.
Paolo medici