Next: Calibrazione secondo Tsai Up: Calibrazione Previous: Calibrazione implicita
Per quanto riguarda il punto di vista computazionale, l'equazione (8.51) è mal condizionata in quanto ogni colonna rappresenta una quantità con un ordine di grandezza differente. Per ottenere dal punto di vista lineare una soluzione corretta è richiesta una fase precedente di normalizzazione. Hartley e Zisserman (HZ04) ricordano che la normalizzazione nella DLT è un passo essenziale e non si può ritenere puramente opzionale.
Il calcolo dell'omografia in equazione (8.52) tuttavia ha il difetto di non tenere conto dell'errore di misura sui punti. Di fatto la decomposizione SVD minimizza qualcosa che per puro caso assomiglia l'errore sul termine noto (cosa che invece proprio non viene fatta nel caso (8.51)) e in ogni caso non si riesce a valutare l'errore sulla matrice dei parametri. In questo caso specifico, dove si minimizza ai minimi quadrati un errore puramente matematico senza corrispondente geometrico, si parla di algebraic least squares (ALS).
Siccome la DLT minimizza un errore algebrico e non geometrico, anche se dal punto di vista computazionale la DLT normalizzata è migliore, potrebbe restituire risultati peggiori dal punto di fitting geometrico dei dati. La versione del sistema (8.51) normalizzato ai minimi quadrati viene indicato con normalized algebraic least squares (NALS).
Per superare il limite del calcolo sull'errore algebrico, è necessario tornare al problema originale e non cercare di trasformarlo in un problema lineare ma risolverlo, per esempio in maniera iterativa, attraverso un minimizzatore non lineare.
Se il rumore è presente solo su una delle due immagini, una funzione costo appropriata, con significato geometrico, è la distanza euclidea tra i punti misurati e i punti trasformati.
Questo è chiamato normalmente errore di trasferimento (transfer error) e minimizza una funzione costo non lineare della forma
Tuttavia quando entrambi i dati sono affetti da rumore la funzione costo (8.57) non è ottimale.
Il modo più semplice per estendere la soluzione precedente consiste nel cercare di minimizzare l'errore di trasferimento diretto e l'errore di trasferimento inverso (symmetric transfer error):
| (8.58) |
Questa tuttavia, non è ancora la soluzione ottima, almeno dal punto di vista statistico. Uno stimatore a massima verosomiglianza deve infatti considerare correttamente il rumore su entrambi i dati quando presente (quello che Hartley e Zisserman chiamano Gold Standard). La soluzione alternativa, di fatto quella più corretta, consiste nel minimizzare l'errore di Riproiezione.
Questa soluzione incrementa di molto la dimensione del problema in quanto si pone come obiettivo (o comunque richiede tra le incognite) anche quello di individuare i punti ottimi non affetti da rumore
![]() e
e
![]() :
:
| (8.59) |
Nel caso ancora più generale con rumore di covarianza misurato per ogni singolo punto la metrica corretta è la distanza di mahalanobis (vedi sezione 2.4):
| (8.60) |
Essendo una minimizzazione non lineare è richiesta tuttavia una soluzione iniziale da cui partire per trovare il minimo che soddisfa l'equazione costo: la soluzione lineare è ancora utile ed è usata come spunto iniziale per individuare un minimo sotto una metrica differente.
Lo stimatore MLE richiede l'uso di una variabile sussidiaria
![]() in più per ogni punto e tecniche iterative per risolvere il problema.
È possibile usare come approssimazione della distanza geometrica, l'errore di Sampson, sezione 3.3.7.
Il vincolo omografico (1.75) che lega i punti delle due immagini può essere scritto sotto forma di varietà
in più per ogni punto e tecniche iterative per risolvere il problema.
È possibile usare come approssimazione della distanza geometrica, l'errore di Sampson, sezione 3.3.7.
Il vincolo omografico (1.75) che lega i punti delle due immagini può essere scritto sotto forma di varietà ![]() bidimensionale
bidimensionale
 |
(8.61) |
Nel caso di errore su una singola immagine per calcolare come l'errore si propaga sulla matrice ![]() è necessario calcolare lo Jacobiano della funzione costo (8.57). Esplicitando la trasformazione omografica si ottiene (HZ04)
è necessario calcolare lo Jacobiano della funzione costo (8.57). Esplicitando la trasformazione omografica si ottiene (HZ04)
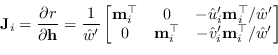 |
(8.63) |
| (8.64) |
Paolo medici